Exercise 1E RS Aggarwal Class 9 contains a total of ten questions. The questions are based on the following topics:
- Representing Irrational numbers on the number line
- Existence of for a given positive real number x
- Representing real numbers on the number line
- Successive Magnification
Exercise 1E RS Aggarwal Class 9 Solutions
The first question of Exercise 1E RS Aggarwal Class 9 is representation of the irrational number on the number line.
1. Represent on the number line.
Answer
Since = = .
As '5' is expressible as the sum of the squares of two numbers, we can follow the following steps to represent it on the number line.
Steps to represent on the number line.
Step 1:
First, we draw a number line and mark two units on it. OA = 2 units.
Step 2:
Secondly, we draw a perpendicular line segment AB, measuring 1 unit, to the number line at point A. AB = 1 units.
Step 3:
Now, we join OB. And with O as centre and OB as radius, we draw an arc, meeting OX at C.
Here, we have followed Pythagoras Theorem to represent on the number line.
Clearly, = = 4 + 1 = 5
⇒ .
So, OB = OC = .
Thus, we have located square root of 5 on the number line.
In Exercise 1E RS Aggarwal Class 9, the second question asks you to find the point on the number line where the square root of 3 is located.
2. Locate on the number line.
Answer
We can write = = =
To represent on the number line, we will start with the representation of first and then we will be able to find the location of on the number line.
Steps to locate on the number line
Step 1:
First, we draw a 1-unit line segment OA on the number line. Then, we draw a perpendicular 1-unit line segment AB at A. Finally, we join OB.
Here, OB = .
Step 2:
We draw a line segment BC of unit length perpendicular to the line segment OB. Then, we join OC.
Here, OC = . We only need to project the line segment OC onto the number line using a compass.
Step 3:
Taking O as the center and OC as the radius, we draw an arc that intersects the number line at D.
Here, OD represents the square root of 3. We have located the square root of 3 on the number line, which lies between 1 and 2. Its approximate value is 1.732. Therefore, it is true.
In Exercise 1E RS Aggarwal Class 9, the third question asks you to find the point on the number line where the square root of 10 is located.
3. Locate on the number line.
Answer
Since = = .
As '10' is expressible as the sum of the squares of two numbers, we can follow the following steps to represent it on the number line.
Steps to represent on the number line.
Step 1:
First, we draw a number line and mark three units on it. OA = 3 units.
Step 2:
Secondly, we draw a perpendicular line segment AB, measuring 1 unit, at point A on the number line.
Step 3:
Now, we join OB. And with O as centre and OB as radius, we draw an arc, meeting OX at C.
Here, we have followed Pythagoras Theorem to represent on the number line.
Clearly, = = 4 + 1 = 5
⇒ .
So, OB = OC = .
Thus, we have located square root of 10 on the number line.
In Exercise 1E RS Aggarwal Class 9, the fourth question asks you to find the point on the number line where the square root of 8 is located.
4. Locate on the number line.
Answer
Since = = .
As '8' is expressible as the sum of the squares of two numbers, we can follow the following steps to represent it on the number line.
Step 1:
First, we draw a number line and mark two units on it. OA = 2 units.
Step 2:
Secondly, we draw a perpendicular line segment AB, measuring 2 units, to the number line at point A. AB = 2 units. We join OB which is equal to .
Step 3:
With O as centre and OB as radius, we draw an arc, meeting OX at C.
Here, we have followed Pythagoras Theorem to represent on the number line.
Here, OAB is a right angled triangle. So,
= = 4 + 4 = 8
⇒ .
So, OB = OC = .
Thus, we have located square root of 8 on the number line.
In Exercise 1E RS Aggarwal Class 9, the fifth question asks you to find the point on the number line where the square root of 4.7 is located.
5. Represent geometrically on the number line.
Answer
The steps to represent geometrically are as follows.
Step 1: First, we draw a line segment AB of length 4.7 cm. Then, we extend the line segment AB by 1 cm such that AC = 4.7 +1 = 5.7 cm.
Step 2: Now, we find the mid-point D of AC using compass by drawing a line bisector of the line segment AC. Steps for drawing a perpendicular bisector is shown below.
Step 3: Now, we draw a semicircle with a radius equal to AD or DC.
Step 4: Draw a perpendicular line from point B to the line AC, where it intersects the semicircle at point E.
Step 5: Finally, we draw an arc taking BE as radius and B as its centre. We extend the line AC to meet the arc at F. So, BF is the required length equal to . We must know that B is the point 0 on the number line and C is 1.
In Exercise 1E RS Aggarwal Class 9, the sixth question asks you to find the point on the number line where the square root of 10.5 is located.
6. Represent on the number line.
Answer
The steps to represent geometrically are as follows.
Step 1: First, we draw a line segment AB of length 10.5 cm. Then, we extend the line segment AB by 1 cm such that AC = 10.5 +1 = 11.5 cm.
Step 2: Now, we find the mid-point of AC using compass by drawing a line bisector of the line segment AC. Steps for drawing a perpendicular bisector is shown below.
Step 3: Now, we draw a semicircle with a radius equal to AD or DC.
Step 4: Draw a perpendicular line from point B to the line AC, where it intersects the semicircle at point E.
Step 5: Finally, we draw an arc taking BE as radius and B as its centre. We extend the line AC to meet the arc at F. So, lies between 3 and 4. We must know that B is the point 0 on the number line and C is 1.
In Exercise 1E RS Aggarwal Class 9, the seventh question asks you to find the point on the number line where the square root of 7.28 is located.
7. Represent geometrically on the number line.
Answer
The steps to represent geometrically are as follows.
Step 1: First, we draw a line segment AB of length 7.28 cm. Then, we extend the line segment AB by 1 cm such that AC = 7.28 +1 = 8.28 cm.
Step 2: Now, we find the mid-point of AC using compass by drawing a line bisector of the line segment AC.
Step 3: Now, we draw a semicircle with a radius equal to AD or DC.
Step 4: Draw a perpendicular line from point B to the line AC, where it intersects the semicircle at point E.
Step 5: Finally, we draw an arc taking BE as radius and B as its centre. We extend the line AC to meet the arc at F. So, lies between 2 and 3. We must know that B is the point 0 on the number line and C is 1.
In Exercise 1E RS Aggarwal Class 9, the eighth question asks you to find the point on the number line where is located.
8. Represent on the number line.
Answer
To represent (1+) on the number line, we first find the position of on the number line as we have done in the other questions of this exercise and then we extend 1 cm more to find the position of 1 + .
The steps to represent geometrically are as follows.
Step 1: First, we draw a line segment AB of length 9.5 cm. Then, we extend the line segment AB by 1 cm such that AC = 9.5 +1 = 10.5 cm.
Step 2: Now, we find the mid-point of AC using compass by drawing a line bisector of the line segment AC.
Step 3: Now, we draw a semicircle with a radius equal to AD or DC.
Step 4: Draw a perpendicular line from point B to the line AC, where it intersects the semicircle at point E.
Step 5: Finally, we draw an arc taking BE as radius and B as its centre. We extend the line AC to meet the arc at F. Thus, we have found the position of on the number line. Now, we have to extend 1cm further to represent the point 1+.
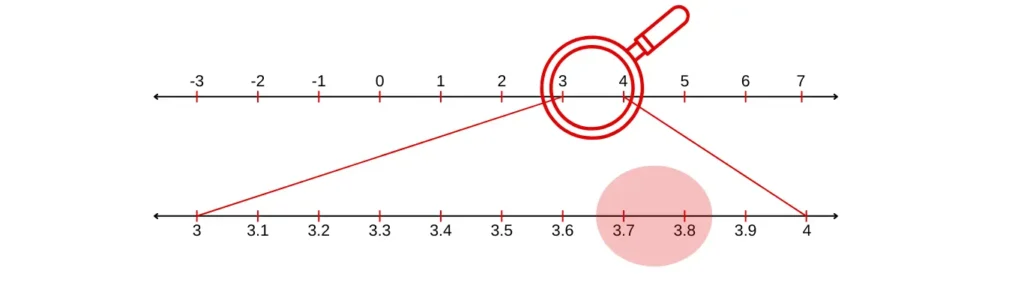
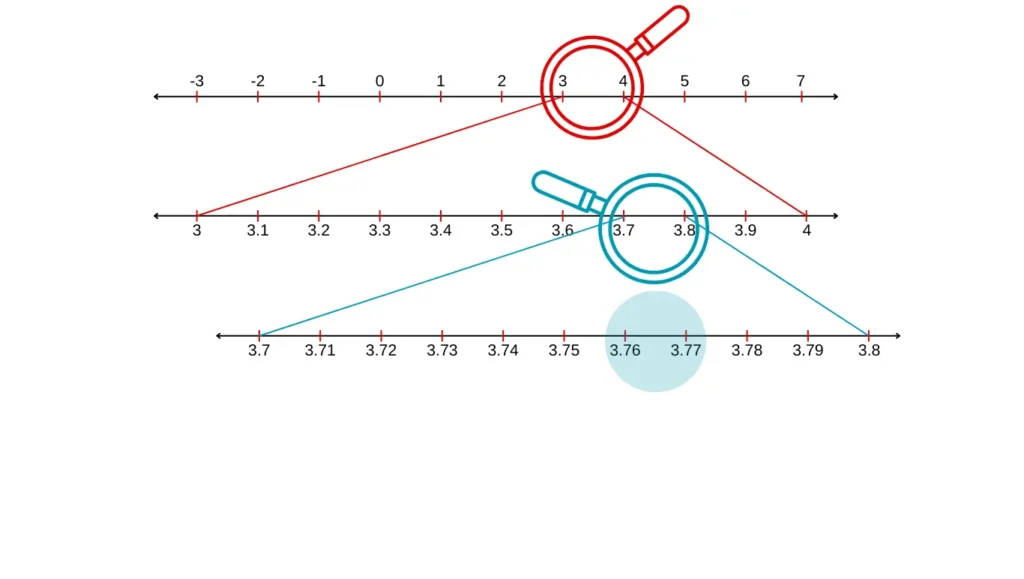
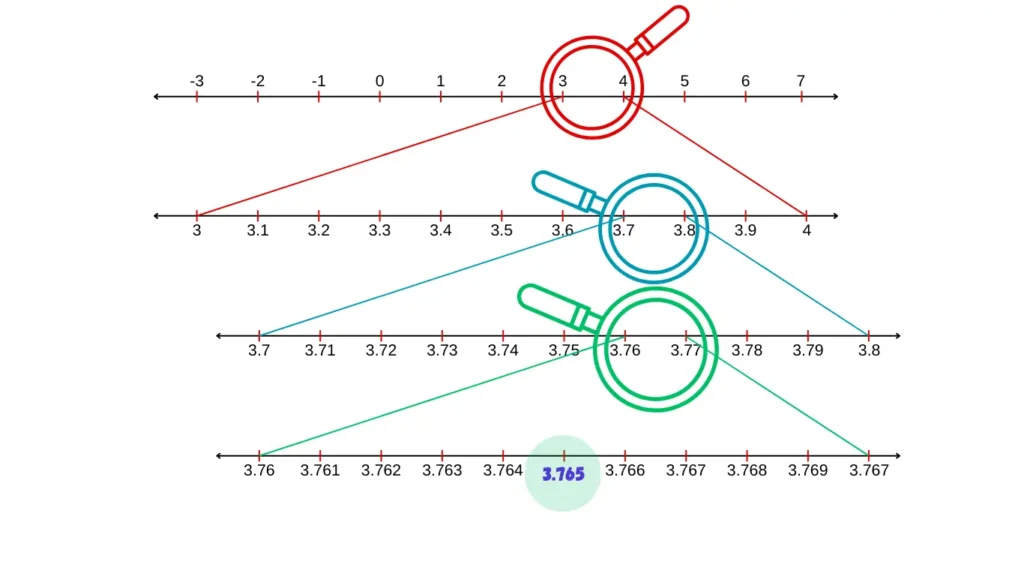
In Exercise 1E RS Aggarwal Class 9, the ninth question asks you to visualize the representation of 3.765 on the number line using successive magnification.
9. Visualize the representation of 3.765 on the number line using successive magnification.
Answer
To visualize means to create a mental image of the number. To visualize 3.765 on the number line, we proceed stepwise as follows.
Step 1: 3.765 lies between 3 and 4. We divide this into 10 equal divisions and mark them as 3.1, 3.2, 3.3, ..., and so on as shown in the following figure.
Step 2: 3.765 lies between 3.7 and 3.8. We divide this into 10 equal divisions and mark them as 3.71, 3.72, 3.73, ..., and so on as shown in the following figure.
If we look this part of the number line closely, as through a lens, it would appear as shown below.
Step 3: 3.765 lies between 3.76 and 3.77. We divide this into 10 equal divisions and mark them as 3.761, 3.762, 3.763, ..., and so on as shown in the following figure.
The visual representation of the blue color number is accurate, indicating 3.765.
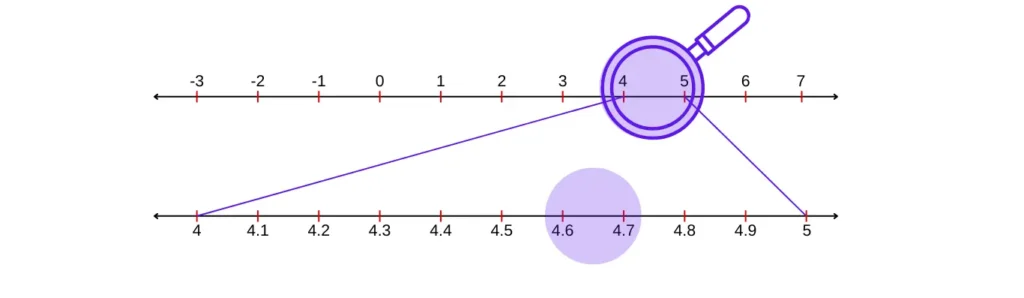
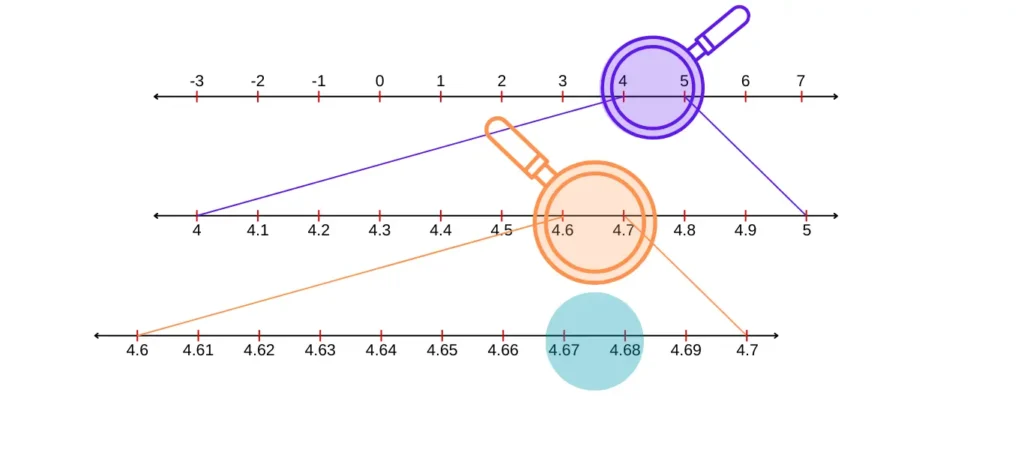
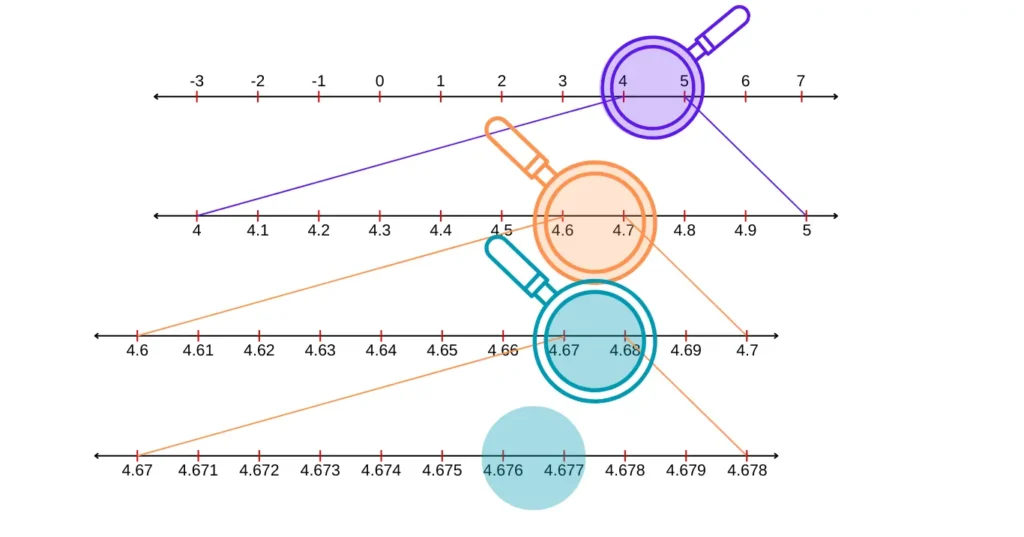
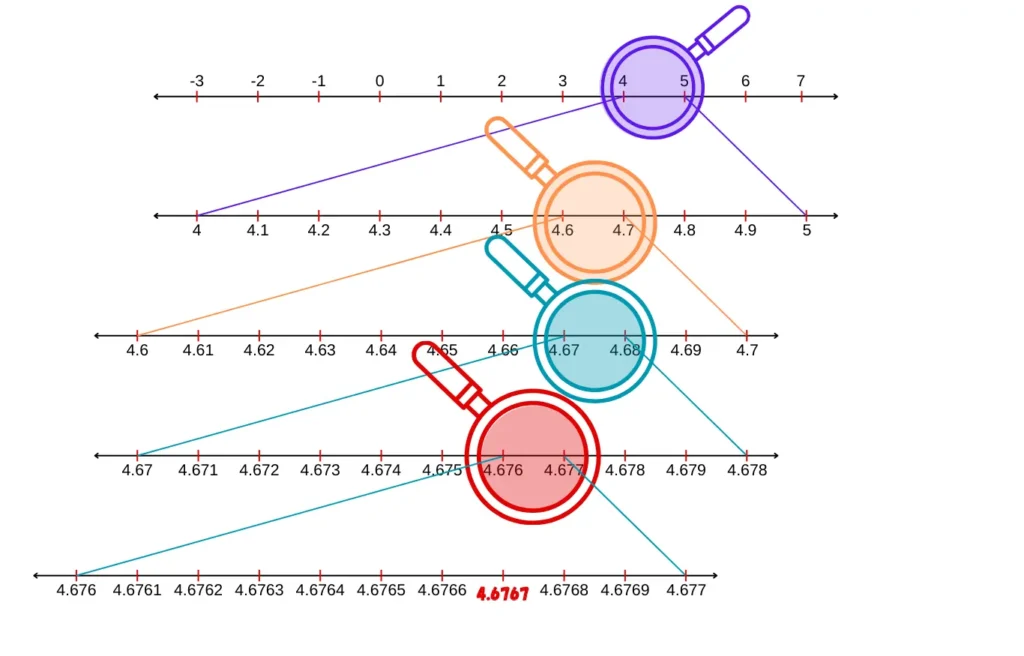
In Exercise 1E RS Aggarwal Class 9, the tenth question asks you to visualize the representation of a rational number on the number line using successive magnification.
10. Visualize the representation of 4.67 on the number line using successive magnification.
Answer
We have 4.67 = 4.6767(unto 4 decimal places)
To visualize means to create a mental image of the number. To visualize 3.765 on the number line, we proceed stepwise as follows.
Step 1: 4.6767 lies between 4 and 5. We divide this into 10 equal divisions and mark them as 4.1, 4.2, 4.3, ..., and so on as shown in the following figure.
Step 2: 4.6767 lies between 4.6 and 4.7. We divide this into 10 equal divisions and mark them as 4.61, 4.62, 4.63, ..., and so on as shown in the following figure.
Step 3: 4.6767 lies between 4.67 and 4.68. We divide this into 10 equal divisions and mark them as 4.671, 4.672, 4.673, ..., and so on as shown in the following figure.
Step 4: 4.6767 lies between 4.676 and 4.677. We divide this into 10 equal divisions and mark them as 4.6761, 4.6762, 4.6763, ..., and so on as shown in the following figure. Thus, we can visualize clearly the point 4.6767 in the figure below.
