Exercise 1B RS Aggarwal Class 9 Best Solutions

Exercise 1A Exercise 1B Exercise 1C Exercise 1D

Exercise 1B RS Aggarwal Class 9 contains a total of five questions. The questions are based on the following topics:

Decimal representation of rational numbers
Terminating Decimal
Repeating (or recurring) decimals
Special characteristics of Rational numbers

Exercise 1B RS Aggarwal Class 9 Solutions

Q.1 Q.2 Q.3 Q.4 Q.5

The first question of Exercise 1B RS Aggarwal Class 9 is based on terminating decimals.

1. Without actual division, find which of the following rational numbers are terminating decimals.

(i) $\frac{13}{80}$

Answer

We know that a rational number in the form of $\frac{p}{q}$ is terminating when $q$ has 2 or 5 as its only factors.

We have, 80 = 2×2×2×2×5 = $2^{4} \times 5^{1}$ .
Here, the denominator of the fraction $\frac{13}{80}$ has 2 or 5 as its only factors.
So, $\frac{13}{80}$ has terminating decimal expansion.

(ii) $\frac{7}{24}$

Answer

We know that a rational number in the form of $\frac{p}{q}$ is terminating when $q$ has 2 or 5 as its only factors.

We have 24 = 2×2×2×3 = $2^{3} \times 3^{1}$ .
Here, the denominator of the fraction $\frac{7}{24}$ has 3 as one of its factors. We have got a factor other than 2 or 5.
So, $\frac{7}{24}$ has a non-terminating and recurring decimal expansion.

(iii) $\frac{5}{12}$

Answer

We know that a rational number in the form of $\frac{p}{q}$ is terminating when the denominator $q$ has 2 or 5 as its only factors.

We have 12 = 2×2×3 = $2^{2} \times 3^{1}$ .
Here, the denominator of the fraction $\frac{5}{12}$ has 3 as one of its factors. It means we have got a factor other than 2 or 5.
So, $\frac{5}{12}$ has a non-terminating and recurring decimal expansion.

(iv) $\frac{31}{375}$

Answer

We know that a rational number in the form of $\frac{p}{q}$ is terminating when the denominator $q$ has 2 or 5 as its only factors.

We have 375 = 5×5×5×3 = $5^{3} \times 3^{1}$ .
Here, the denominator of the fraction $\frac{31}{375}$ has 3 as one of its factors. It means we have got a factor other than 2 or 5.
So, $\frac{31}{375}$ has a non-terminating and recurring decimal expansion.

(v) $\frac{16}{125}$

Answer

We know that a rational number in the form of $\frac{p}{q}$ is terminating when the denominator $q$ has 2 or 5 as its only factors.

We have 125 = 5×5×5 = $5^{3}$ .
Here, the denominator of the fraction $\frac{16}{125}$ has 5 as its only factor.
So, $\frac{16}{125}$ has a terminating decimal expansion.

The second question of Exercise 1B RS Aggarwal Class 9 is based conversion of a rational numbers into a decimal expansion.

2. Write each of the following in decimal form and say what kind of decimal expansion each has.

(i) $\frac{5}{8}$

Answer

The decimal form of $\frac{5}{8}$ = 0.625.
It is a terminating decimal expansion.

(ii) $\frac{7}{25}$

Answer

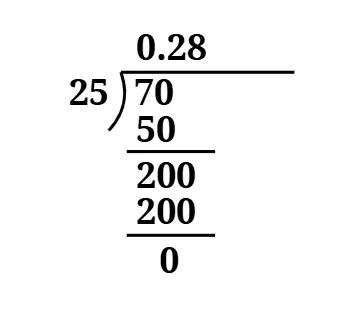
The decimal form of $\frac{7}{25}$ = 0.28.
It is a terminating decimal expansion.

(iii) $\frac{3}{11}$

Answer

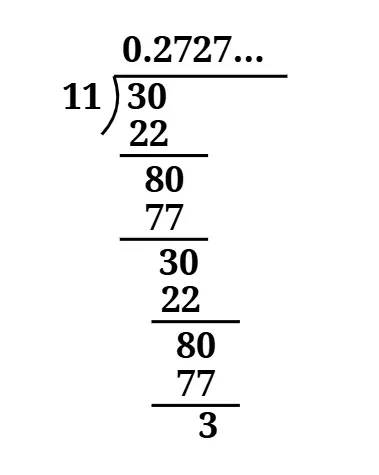
The decimal form of $\frac{3}{11}$ = 0.2727... = 0.27.
It is a non-terminating and recurring decimal expansion.

(iv) $\frac{5}{13}$

Answer

The decimal form of $\frac{5}{13}$ = 0.384615384615... = 0.384615.
It is a non-terminating and recurring decimal expansion.

(v) $\frac{11}{24}$

Answer

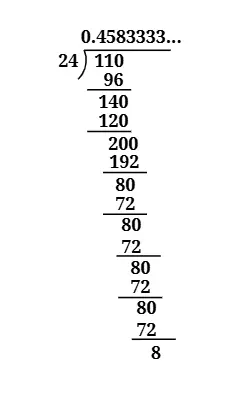
The decimal form of $\frac{11}{24}$ = 0.458333... = 0.4583.
It is a non-terminating and recurring decimal expansion.

(vi) $\frac{261}{400}$

Answer

The decimal form of $\frac{261}{400}$ = 0.6525.
It is a terminating decimal expansion.

(vii) $\frac{231}{625}$

Answer

The decimal form of $\frac{231}{625}$ = 0.3696.
It is a terminating decimal expansion.

(viii) $2 \frac{5}{12}$

Answer

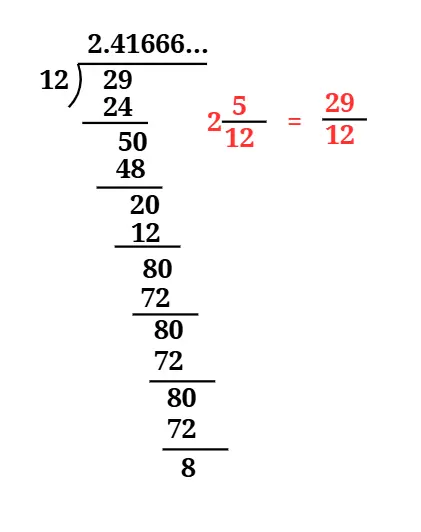
The decimal form of $2 \frac{5}{12}$ = 2.41666... = 2.416
It is a non-terminating and recurring decimal expansion.

The third question of Exercise 1B RS Aggarwal Class 9 is based conversion of a decimal form of a rational number to $\frac{p}{q}$ form

3. Express each of the following decimals in the form $\frac{p}{q}$ , where $p, q$ are integers and $q \neq 0$ .

(i) 0.2

Answer

Let $x$ = 0.2
$\Rightarrow x = 0.222 . . .$ ----->(1)
$\Rightarrow 10 x = 2.222 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

10 x = 2.222 . . .

x = 0.222 . . .

9 x = 2.000 . . .

\Rightarrow 9 x = 2

\Rightarrow x = \frac{2}{9}

Hence, 0.2 =

\frac{2}{9}

(ii) 0.53

Answer

Let $x$ = 0.53
$\Rightarrow x = 0.535353 . . .$ ----->(1)
$\Rightarrow 100 x = 53.535353 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 53.535353 . . .

x = 0.535353 . . .

99 x = 53.000 . . .

\Rightarrow 99 x = 53

\Rightarrow x = \frac{53}{99}

Hence, 0.53 =

\frac{53}{99}

(iii) 2.93

Answer

Let $x$ = 2.93
$\Rightarrow x = 2.939393 . . .$ ----->(1)
$\Rightarrow 100 x = 293.939393 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 293.939393. . .

x = 2.939393 . . .

99 x = 291.000 . . .

\Rightarrow 99 x = 291

\Rightarrow x = \frac{291}{99}

\Rightarrow x = \frac{97}{33}

Hence, 2.93 =

\frac{97}{33}

(iv) 18.48

Answer

Let $x$ = 18.48
$\Rightarrow x = 18.484848 . . .$ ----->(1)
$\Rightarrow 100 x = 1848.484848 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 1848.484848 . . .

x = 18.484848 . . .

99 x = 1830.000 . . .

\Rightarrow 99 x = 1830

\Rightarrow x = \frac{1830}{99}

\Rightarrow x = \frac{610}{33}

Hence, 18.48 =

\frac{610}{33}

(v) 0.235

Answer

Let $x$ = 0.235
$\Rightarrow x = 0.235235235 . . .$ ----->(1)
$\Rightarrow 1000 x = 235.235235235 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

1000 x = 235.235235235 . . .

x = 0.235235235 . . .

999 x = 235.000 . . .

\Rightarrow 999 x = 235

\Rightarrow x = \frac{235}{999}

Hence, 0.235 =

\frac{235}{999}

(vi) 0.0032

Answer

Let $x$ = 0.0032
$\Rightarrow x = 0.00323232 . . .$ ----->(1)
$\Rightarrow 100 x = 0.323232 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 0.323232. . .

x = 0.003232 . . .

99 x = 0.320000 . . .

\Rightarrow x = \frac{0.32}{99}

\Rightarrow x = \frac{0.32 \times 100}{99 \times 100}

\Rightarrow x = \frac{32}{9900}

\Rightarrow x = \frac{8}{2475}

Hence, 0.0032 =

\frac{8}{2475}

(vii) 1.323

Answer

Let $x$ = 1.323
$\Rightarrow x = 1.3232323 . . .$ ----->(1)
$\Rightarrow 100 x = 132.3232323 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 132.3232323. . .

x = 1.3232323 . . .

99 x = 131

\Rightarrow x = \frac{131}{99}

Hence, 1.323 =

\frac{131}{99}

(viii) 0.3178

Answer

Let $x$ = 0.3178
$\Rightarrow x = 0.3178178178 . . .$ ----->(1)
$\Rightarrow 1000 x = 317.8178178178 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

1000 x = 317.8178178178. . .

x = 0.3178178178 . . .

999 x = 317.5000000000 . . .

\Rightarrow x = \frac{317.5}{999}

\Rightarrow x = \frac{317.5 \times 10}{999 \times 10}

\Rightarrow x = \frac{3175}{9990}

\Rightarrow x = \frac{635}{1998}

Hence, 0.3178 =

\frac{635}{1998}

(ix) 32.1235

Answer

Let $x$ = 32.1235
$\Rightarrow x = 32.12353535 . . .$ ----->(1)
$\Rightarrow 100 x = 3212.353535 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 3212.35353535. . .

x = 32.12353535 . . .

99 x = 3180.23 . . .

\Rightarrow x = \frac{3180.23}{99}

\Rightarrow x = \frac{3180.23 \times 100}{99 \times 100}

\Rightarrow x = \frac{318023}{9900}

Hence, 32.1235 =

\frac{318023}{9900}

(x) 0.407

Answer

Let $x$ = 0.407
$\Rightarrow x = 0.40777 . . .$ ----->(1)
$\Rightarrow 10 x = 4.07777 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

10 x = 4.07777 . . .

x = 0.40777. . .

9 x = 3.67000 . . .

\Rightarrow 9 x = 3.67

\Rightarrow x = \frac{3.67}{9}

\Rightarrow x = \frac{3.67 \times 100}{9 \times 100}

\Rightarrow x = \frac{367}{900}

Hence, 0.407 =

\frac{367}{900}

The Fourth question of Exercise 1B RS Aggarwal Class 9 asks to express a rational number in fraction in simplest form.

4. Express 2.36 + 0.23 as a fraction in simplest form.

Answer

We have 2.36 + 0.23 = 2.59.

Let $x$ = 2.59
$\Rightarrow x = 2.595959 . . .$ ----->(1)
$\Rightarrow 100 x = 259.595959 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 259.595959. . .

x = 2.595959 . . .

99 x = 257.000 . . .

\Rightarrow 99 x = 257

\Rightarrow x = \frac{257}{99}

Hence, 2.59 =

\frac{257}{99}

The fifth question of Exercise 1B RS Aggarwal Class 9 asks to express a rational number in fraction in simplest form.

5. Express in the form of $\frac{p}{q} :$ 0.38 + 1.27.

Answer

We have 0.38 + 1.27 = 1.65.

Let $x$ = 1.65
$\Rightarrow x = 1.656565 . . .$ ----->(1)
$\Rightarrow 100 x = 259.595959 . . .$ ----->(2)

Subtracting equation (1) from equation (2), we get

100 x = 165.656565. . .

x = 1.656565 . . .

99 x = 164.000000 . . .

\Rightarrow 99 x = 164

\Rightarrow x = \frac{164}{99}

Hence, 1.65 =

\frac{164}{99}

Exercise 1B RS Aggarwal Class 9 Solutions

1. Without actual division, find which of the following rational numbers are terminating decimals.

(i) 1380

Answer

(ii) 724

Answer

(iii) 512

Answer

(iv) 31375

Answer

(v) 16125

Answer

2. Write each of the following in decimal form and say what kind of decimal expansion each has.

(i) 58

Answer

(ii) 725

Answer

(iii) 311

Answer

(iv) 513

Answer

(v) 1124

Answer

(vi) 261400

Answer

(vii) 231625

Answer

(viii) 2512

Answer

3. Express each of the following decimals in the form pq, where p,q are integers and q ≠ 0.

(i) 0.2

Answer

(ii) 0.53

Answer

(iii) 2.93

Answer

(iv) 18.48

Answer

(v) 0.235

Answer

(vi) 0.0032

Answer

(vii) 1.323

Answer

(viii) 0.3178

Answer

(ix) 32.1235

Answer

(x) 0.407

Answer

4. Express 2.36 + 0.23 as a fraction in simplest form.

Answer

5. Express in the form of pq: 0.38 + 1.27.

Answer

Important Links

(i) $\frac{13}{80}$

(ii) $\frac{7}{24}$

(iii) $\frac{5}{12}$

(iv) $\frac{31}{375}$

(v) $\frac{16}{125}$

(i) $\frac{5}{8}$

(ii) $\frac{7}{25}$

(iii) $\frac{3}{11}$

(iv) $\frac{5}{13}$

(v) $\frac{11}{24}$

(vi) $\frac{261}{400}$

(vii) $\frac{231}{625}$

(viii) $2 \frac{5}{12}$

3. Express each of the following decimals in the form $\frac{p}{q}$ , where $p, q$ are integers and $q \neq 0$ .

5. Express in the form of $\frac{p}{q} :$ 0.38 + 1.27.