
Exercise 1.5 NCERT Class 11 contains 7 questions. Each question contains several small questions. And each question of exercise 1.5 NCERT Class 11 is easy to solve if concepts are clear. The solutions to each and every question are given below.
All previous exercises, like Exercise 1.1, Exercise 1.2, and Exercise 1.3, have already been completed.
Exercise 1.5 NCERT Class 11 Mathematics Solutions
The first question of Exercise 1.5 NCERT Class 11 is about finding the complement of a set.
1. Let U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {1, 2, 3, 4}, B = {2, 4, 6, 8} and C = {3, 4, 5, 6}. Find
(i) A'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
So, A' = U − A = {5, 6, 7, 8, 9}
(ii) B'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {2, 4, 6, 8}
So, B' = U − B = {1, 3, 5, 7, 9}
(iii) (A ∪ C)'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
C = {3, 4, 5, 6}
A ∪ C = {1, 2, 3, 4, 5, 6}
So, (A ∪ C)' = U − (A ∪ C) = {7, 8, 9}
(iv) (A ∪ B)'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
B = {2, 4, 6, 8}
A ∪ B = {1, 2, 3, 4, 6, 8}
So, (A ∪ B)' = U − (A ∪ B) = {5, 7, 9}
(v) (A')'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {1, 2, 3, 4}
So, A' = U − A = {5, 6, 7, 8, 9}
and (A')' = U − A' = {1, 2, 3, 4}
(vi) (B − C)'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {2, 4, 6, 8}
C = {3, 4, 5, 6}
So, B − C = {2, 8}
Now, (B − C)' = U − (B − C) = {1, 3, 4, 5, 6, 7, 9}
The second question of Exercise 1.5 NCERT Class 11 is also about finding the complement of a set.
2. If U = , find the complements of the following sets:
(i) A =
Answer
Here, U =
A =
∴ Complement of A = A' = U − A =
(ii) B =
Answer
Here, U =
B =
∴ Complement of B = B' = U − B =
(iii) C =
Answer
Here, U =
C =
∴ Complement of C = C' = U − C =
(iv) D =
Answer
Here, U =
D =
∴ Complement of D = D' = U − D =
The third question of Exercise 1.5 NCERT Class 11 is also about finding the complement of a set by taking set of natural numbers as universal set.
3. Taking the set of natural numbers as the universal set, write down the complements of the following sets:
(i)
Answer
Let A =
Clearly, if we exclude the even natural numbers from the set of natural numbers, we get the set of odd natural numbers.
So, complement of A = A' = N − A = .
(ii)
Answer
Let A =
Clearly, if we exclude the odd natural numbers from the set of natural numbers, we get the set of even natural numbers.
So, complement of A = A' = N − A = .
(iii)
Answer
Let A =
A = {3, 6, 9, 12, 15, 18, . . . }
Clearly, the complement of set A contains all those natural numbers that are not multiples of 3.
So, A' = N − A = {1, 2, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, . . . }
A' =
(iv)
Answer
Let A =
A = {2, 3, 5, 7, 11, 13, 17, . . .}
So, A' = N − A = {1, 4, 6, 8, 9, 10, 12, 14, 15, 16}
We see that A' contains all composite numbers and 1 that is not a composite number.
∴ A' =
(v)
Answer
Let A =
The natural numbers that are divisible by 3 and 5 are those numbers that are multiple of the LCM of 3 and 5.
In Roster form, we can write
A = {15, 30, 45, 60, 75, 90, . . .}
A' = N − A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 17, 18, 19, . . .}
In Roster form, we can write
A' =
(vi)
Answer
Let A =
A = {1, 4, 9, 16, 25 . . .}
A' = N − A = {2, 3, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 17, . . .}
In Roster form, we can write
A' =
(vii)
Answer
Let A =
⇒ A = {1, 8, 27, . . .}
∴ A' = N − A = {2, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 28, . . .}
⇒ A' =
(viii)
Answer
Let A =
⇒ A = {3}
∴ A' = N − A = {1, 2, 4, 5, 6, 7, . . .}
⇒ A' =
(ix)
Answer
Let A =
From the given set, we have
⇒
⇒
∴ A = {2}
⇒ A' = N − A = {1, 3, 4, 5, 6, . . .}
⇒ A' =
(x)
Answer
Let A =
∴ A = {7, 8, 9, 10, 11, . . .}
⇒ A' = N − A = {1, 2, 3, 4, 5, 6}
⇒ A' =
(xi)
Answer
Let A =
From the given set, we have
The fourth question of Exercise 1.5 NCERT Class 11 is to verify the equalities called De Morgan's laws. The laws state that the complement of the union of two sets is the intersection of their complements and the complement of the intersection of two sets is the union of their complements.
4. If U = {1, 2, 3, 4, 5, 6, 7, 8, 9}, A = {2, 4, 6, 8} and B = {2, 3, 5, 7}. Verify that
(i) (A ∪ B)' = A' ∩ B'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
B = {2, 3, 5, 7}
So, A ∪ B = {2, 3, 4, 5, 6, 7, 8}
To verify: (A ∪ B)' = A' ∩ B'
Taking LHS,
(A ∪ B)' = U − (A ∪ B) = {1, 9}
Taking RHS,
A' ∩ B' = (U − A) ∩ (U − B)
= {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9}
= {1, 9}
∴LHS = RHS, Hence Proved
(ii) (A ∩ B)' = A' ∪ B'
Answer
Here, U = {1, 2, 3, 4, 5, 6, 7, 8, 9}
A = {2, 4, 6, 8}
B = {2, 3, 5, 7}
So, A ∩ B = {2}
To verify: (A ∩ B)' = A' ∪ B'
Taking LHS,
(A ∩ B)' = U − (A ∩ B) = {1, 3, 4, 5, 6, 7, 8, 9}
Taking RHS,
A' ∪ B' = (U − A) ∪ (U − B)
= {1, 3, 5, 7, 9} ∩ {1, 4, 6, 8, 9}
= {1, 3, 4, 5, 6, 7, 8, 9}
∴LHS = RHS, Hence Proved
The fifth question of Exercise 1.5 NCERT Class 11 asks to draw Venn diagram of given sets. Venn diagrams consist of rectangles and closed curves usually circles. The universal set is represented usually by a rectangle and its subsets by circles.
5. Draw appropriate Venn diagram for each of the following:
(i) (A ∪ B)'
Answer
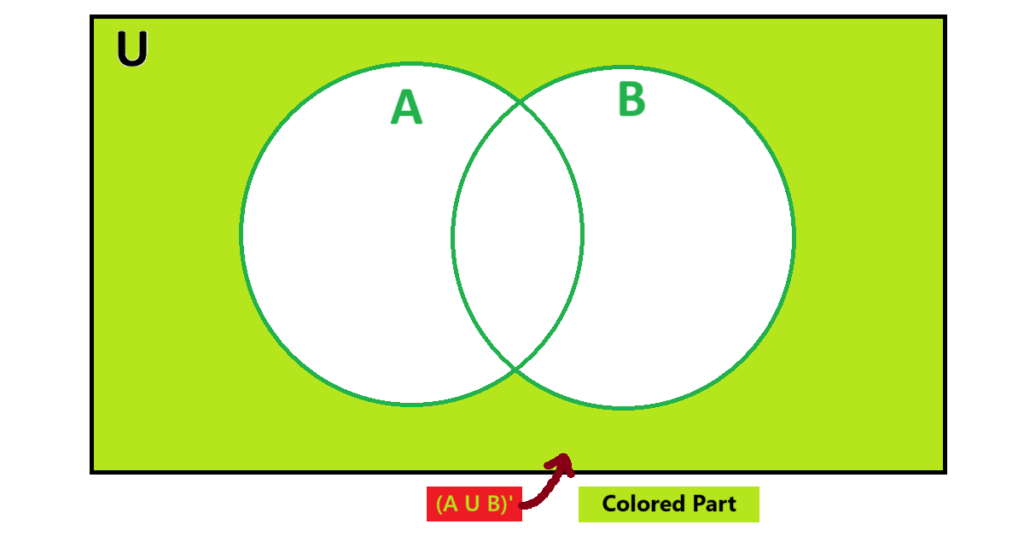
(ii) A' ∩ B'
Answer
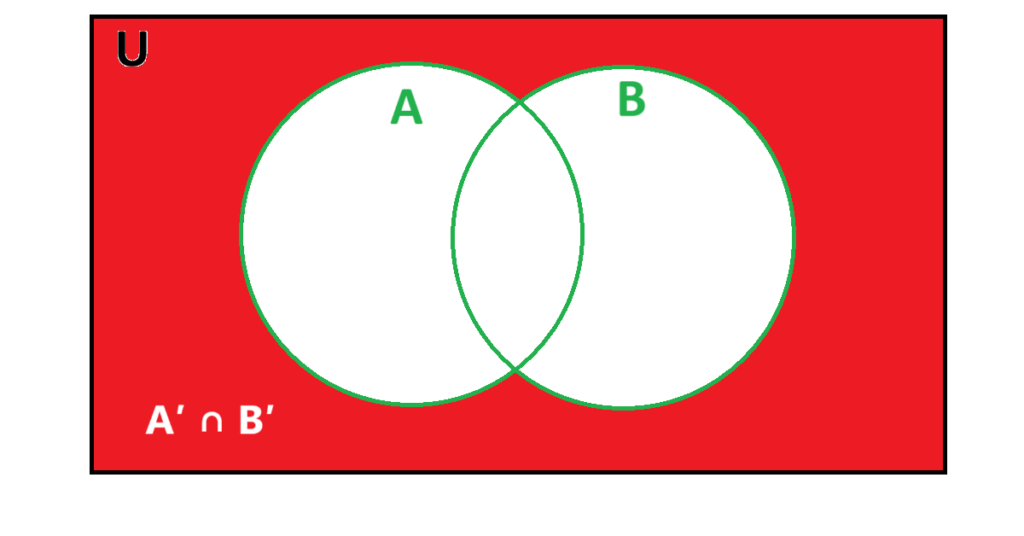
(iii) (A ∩ B)'
Answer
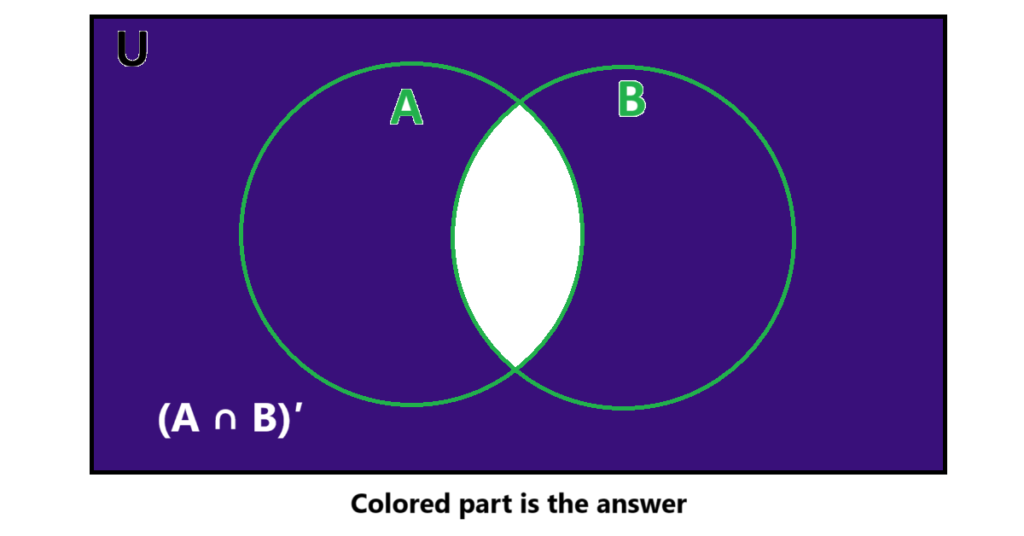
(iv) A' ∪ B'
Answer
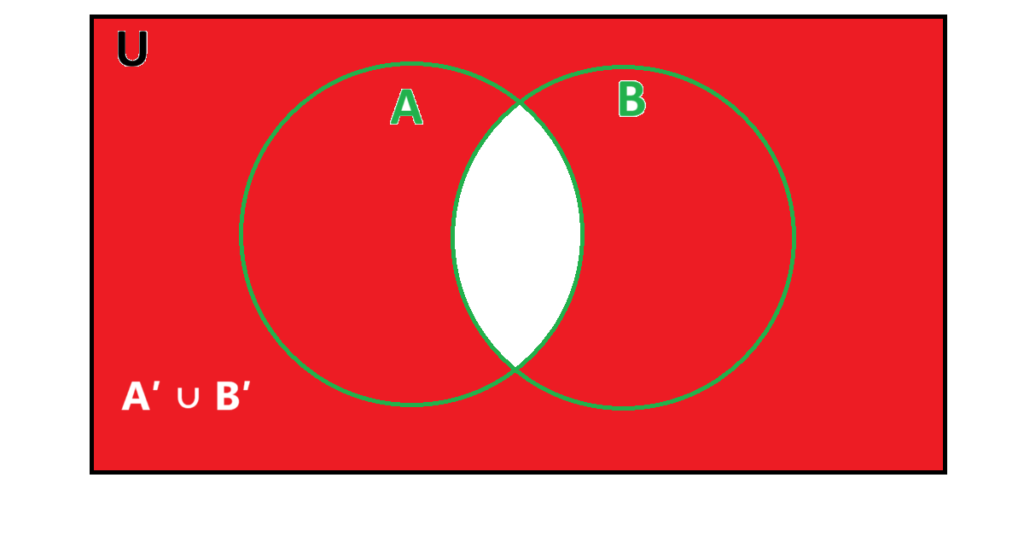
The sixth question of Exercise 1.5 NCERT Class 11 asks to find the complement of set A.
6. Let U be the set of all triangles in a plane. If A is the set of all triangles with at least one angle different from 60 °
Answer
Here, U = the set of all triangles in a plane.
A = The set of all triangles with at least one angle different from 60°.
Clearly, if A is a set of triangles with at least one angle different from 60°, then it's complement should be the set consisting of triangles having all angles 60° and it is an equilateral triangle. So, the answer is
A' = the set of all equilateral triangles.
The sixth question of Exercise 1.5 NCERT Class 11 is about true false questions on complement of sets.
7. Fill in the blanks to make each of the following a true statement:
(i) A ∪ A' = . . .
Answer
A ∪ A' = A ∪ (U − A) = U, as it contains all elements of A and also those elements that are not in it but are in U.
(ii) ϕ '
Answer
ϕ' ∩ A = (U − ϕ) ∩ A = U ∩ A = A
(iii) A ∩ A' = . . .
Answer
A ∩ A' = A ∩ (U − A) = ϕ
(iv) U' ∩ A = . . .
Answer
U' ∩ A = (U − U) ∩ A = ϕ ∩ A = ϕ
