Exercise 1.4 NCERT Class 9 Number Systems Best Solutions

Exercise 1.1 Exercise 1.2 Exercise 1.3 Exercise 1.4 Exercise 1.5 Exercise 2.1 Exercise 2.2 Exercise 2.3 Exercise 2.4

Exercise 1.4 NCERT Class 9 contains a total of five questions. The questions are based on the following topics.

Operations on Real Numbers

Rationalisation

Download NCERT Class 9 Book

Exercise 1.4 NCERT Class 9 Mathematics Solutions

Q.1 Q.2 Q.3 Q.4 Q.5

The first question of Exercise 1.4 NCERT Class 9 asks to identify whether a number is rational or irrational.

1. Classify the following numbers as rational or irrational:

(i) $2 - \sqrt{5}$

Answer

As we know that the difference of a rational number and an irrational number is an irrational number. So, $2 - \sqrt{5}$ is an irrational number .

(ii) $(3 + \sqrt{23}) - \sqrt{23}$

Answer

We have
$(3 + \sqrt{23}) - \sqrt{23}$ = $3 + \sqrt{23} - \sqrt{23}$ = 3. Clearly, 3 is a rational number.
Hence, $(3 + \sqrt{23}) - \sqrt{23}$ is a rational number.

(iii) $\frac{2 \sqrt{7}}{7 \sqrt{7}}$

Answer

We have
$\frac{2 \sqrt{7}}{7 \sqrt{7}}$ = $\frac{2 \sqrt{7}}{7 \sqrt{7}} = \frac{2}{7}$ . Clearly, $\frac{2}{7}$ is a rational number.
Hence, $\frac{2 \sqrt{7}}{7 \sqrt{7}}$ is a rational number.

(iv) $\frac{1}{\sqrt{2}}$

Answer

We have
$\frac{1}{\sqrt{2}}$ = $\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}$ = $\frac{\sqrt{2}}{2}$ is an irrational number as the quotient obtained by dividing an irrational number by a rational number is an irrational number.

(v) $2 π$

Answer

$2 π$ is an irrational number. It is because $π$ is an irrational number.

The second question of Exercise 1.3 NCERT Class 9 asks to simplify the given surd expressions.

2. Simplify each of the following expressions:

(i) $(3 + \sqrt{3}) (2 + \sqrt{2})$

Answer

We have
$(3 + \sqrt{3}) (2 + \sqrt{2})$
= $3 (2 + \sqrt{2}) + \sqrt{3} (2 + \sqrt{2})$
= $6 + 3 \sqrt{2} + 2 \sqrt{3} + \sqrt{3 \times 2}$
= $6 + 3 \sqrt{2} + 2 \sqrt{3} + \sqrt{6}$

(ii) $(3 + \sqrt{3}) (3 - \sqrt{3})$

Answer

We have
$(3 + \sqrt{3}) (3 - \sqrt{3})$
= $3^{2} - {(\sqrt{3})}^{2}$ ... $[∵ (a + b) (a - b) = a^{2} - b^{2}]$
= $9 - 3$
= $6$

(iii) ${(\sqrt{5} + \sqrt{2})}^{2}$

Answer

We have
${(\sqrt{5} + \sqrt{2})}^{2}$
= ${(\sqrt{5})}^{2} + 2 \times \sqrt{5} \times \sqrt{2} + {(\sqrt{2})}^{2}$ ... $[∵ {(a + b)}^{2} = a^{2} + 2 a b + b^{2}]$
= $5 + 2 \sqrt{5 \times 2} + 2$
= $7 + 2 \sqrt{10}$

(iv) $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2})$

Answer

We have
$(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2})$
= ${(\sqrt{5})}^{2} - {(\sqrt{2})}^{2}$ ... $[∵ (a + b) (a - b) = a^{2} - b^{2}]$
= $5 - 2$
= $3$

The third question of Exercise 1.4 NCERT Class 9 is about $π$ .

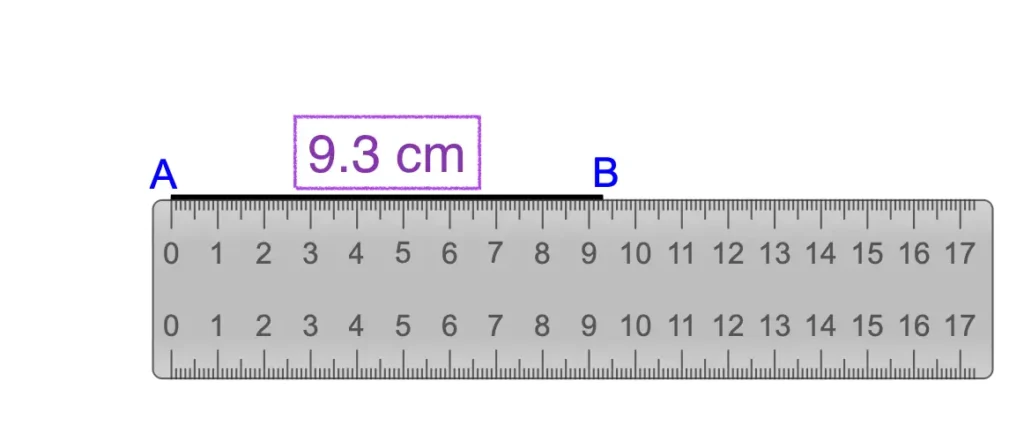
3. Recall, $π$ is defined as the ratio of the circumference (say c) to its diameter (say d). That is, $π = \frac{c}{d}$ . This seems to contradict the fact that $π$ is irrational. How will you resolve this contradiction?

Answer

There’s no contradiction. Remember, when you measure a length using a scale or any other device, you only obtain an approximate rational value. Consequently, you might not realize that either c or d is irrational.

One potential resolution to this dispute is to consider either the denominator or the numerator to be an irrational number. For instance, if the denominator is set to 2 cm and you attempt to measure the circumference of the circle, you will discover that it is an irrational number.
Analogously, if you assume the circumference is fixed at 4 centimeters and attempt to determine its diameter, you will discover that it is an irrational number.
The conclusion is that one of the values between circumference and diameter is inherently irrational.

The fourth question of Exercise 1.4 NCERT Class 9 is about the representation of a real number in square root on the number line.

4. Represent $\sqrt{9.3}$ on the number line.

Answer

The steps to represent $\sqrt{9.3}$ are as follows.

Step 1: First, we draw a line segment AB of length 9.3 cm.

Step 2: Second, we extend the line segment AB by 1cm such that AC = 9.3 +1 = 10.3 cm.

Step 3: Now, we find the mid-point D of AC using compass by drawing a line bisector of the line segment AC. Steps for drawing a perpendicular bisector has been shown below.

Step 4: Now, we draw a semicircle with a radius equal to AD or DC.

Step 5: We draw a line perpendicular to the line AC at point B where it meets the semicircle at E.

Step 6: Finally, we draw an arc taking BE as radius and B as its centre. We extend the line AC to meet the arc at F. So, BF is the required length equal to $\sqrt{9.3}$ . We must know that B is the point 0 on the number line and C is 1.

The fifth question of Exercise 1.4 NCERT Class 9 is about rationalisation of the denominator in fractions.

5. Rationalise the denominator of the following:

(i) $\frac{1}{\sqrt{7}}$

Answer

We multiply the numerator and denominator by $\sqrt{7}$ to rationalise the denominator of $\frac{1}{\sqrt{7}}$ .
$\frac{1}{\sqrt{7}} = \frac{1 \times \sqrt{7}}{\sqrt{7} \times \sqrt{7}}$ = $\frac{\sqrt{7}}{7}$ .

Rationalizing the denominator entails transforming the numerator or the expression within the denominator into a rational number.

(ii) $\frac{1}{\sqrt{7} - \sqrt{6}}$

Answer

Rationalizing the denominator entails transforming the numerator or the expression within the denominator into a rational number.

WE have
$\frac{1}{\sqrt{7} - \sqrt{6}}$
Multiplying the numerator and denominator by $(\sqrt{7} + \sqrt{6})$ , we get
$\frac{1 \times (\sqrt{7} + \sqrt{6})}{(\sqrt{7} - \sqrt{6}) (\sqrt{7} + \sqrt{6})}$ = $\frac{(\sqrt{7} + \sqrt{6})}{{(\sqrt{7})}^{2} - {(\sqrt{6})}^{2}}$ = $\frac{(\sqrt{7} + \sqrt{6})}{7 - 6}$ = $(\sqrt{7} + \sqrt{6})$

(iii) $\frac{1}{\sqrt{5} + \sqrt{2}}$

Answer

WE have
$\frac{1}{\sqrt{5} + \sqrt{2}}$
Multiplying the numerator and denominator by $(\sqrt{5} - \sqrt{2})$ , we get
$\frac{1 \times (\sqrt{5} - \sqrt{2})}{(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2})}$ = $\frac{(\sqrt{5} - \sqrt{2})}{{(\sqrt{5})}^{2} - {(\sqrt{2})}^{2}}$ = $\frac{(\sqrt{5} - \sqrt{2})}{5 - 2}$ = $\frac{(\sqrt{5} - \sqrt{2})}{3}$

(iv) $\frac{1}{\sqrt{7} - 2}$

Answer

WE have
$\frac{1}{\sqrt{7} - 2}$
Multiplying the numerator and denominator by $(\sqrt{7} + 2)$ , we get
$\frac{1 \times (\sqrt{7} + 2)}{(\sqrt{7} - 2) (\sqrt{7} + 2)}$ = $\frac{(\sqrt{7} + 2)}{{(\sqrt{7})}^{2} - {(2)}^{2}}$ = $\frac{(\sqrt{7} + 2)}{7 - 2}$ = $\frac{(\sqrt{7} + 2)}{5}$

Chapter Test ML Aggarwal Class 9 Rational and Irrational Numbers Full Solutions

Exercise 1.5 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Exercise 1.4 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Polynomial Worksheets Class 9 Mathematics Best for Practice

Exercise 1.3 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Motion NCERT Class 9 Concise Notes and Best Question Answers

Download NCERT Class 9 Book

Exercise 1.4 NCERT Class 9 Mathematics Solutions

1. Classify the following numbers as rational or irrational:

(i) 2−5

Answer

As we know that the difference of a rational number and an irrational number is an irrational number. So, 2−5 is an irrational number .

(ii) (3+23)−23

Answer

We have (3+23)−23 = 3+23−23 = 3. Clearly, 3 is a rational number. Hence, (3+23)−23 is a rational number.

(iii) 2777

Answer

We have 2777 = 2777=27. Clearly, 27 is a rational number. Hence, 2777 is a rational number.

(iv) 12

Answer

We have 12 = 1×22×2 = 22 is an irrational number as the quotient obtained by dividing an irrational number by a rational number is an irrational number.

(v) 2π

Answer

2π is an irrational number. It is because π is an irrational number.

2. Simplify each of the following expressions:

(i) (3+3)(2+2)

Answer

We have (3+3)(2+2) = 3(2+2)+3(2+2) = 6+32+23+3×2 = 6+32+23+6

(ii) (3+3)(3−3)

Answer

We have (3+3)(3−3) = 32−(3)2 ... [∵(a+b)(a−b)=a2−b2] = 9−3 = 6

(iii) (5+2)2

Answer

We have (5+2)2 = (5)2+2×5×2+(2)2 ... [∵(a+b)2=a2+2ab+b2] = 5+25×2+2 = 7+210

(iv) (5+2)(5−2)

Answer

We have (5+2)(5−2) = (5)2−(2)2 ... [∵(a+b)(a−b)=a2−b2] = 5−2 = 3

3. Recall, π is defined as the ratio of the circumference (say c) to its diameter (say d). That is, π=cd. This seems to contradict the fact that π is irrational. How will you resolve this contradiction?

Answer

4. Represent 9.3 on the number line.

Answer

5. Rationalise the denominator of the following:

(i) 17

Answer

(ii) 17−6

Answer

(iii) 15+2

Answer

(iv) 17−2

Answer

Chapter Test ML Aggarwal Class 9 Rational and Irrational Numbers Full Solutions

Exercise 1.5 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Exercise 1.4 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Polynomial Worksheets Class 9 Mathematics Best for Practice

Exercise 1.3 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Motion NCERT Class 9 Concise Notes and Best Question Answers

(i) $2 - \sqrt{5}$

As we know that the difference of a rational number and an irrational number is an irrational number. So, $2 - \sqrt{5}$ is an irrational number .

(ii) $(3 + \sqrt{23}) - \sqrt{23}$

We have
$(3 + \sqrt{23}) - \sqrt{23}$ = $3 + \sqrt{23} - \sqrt{23}$ = 3. Clearly, 3 is a rational number.
Hence, $(3 + \sqrt{23}) - \sqrt{23}$ is a rational number.

(iii) $\frac{2 \sqrt{7}}{7 \sqrt{7}}$

We have
$\frac{2 \sqrt{7}}{7 \sqrt{7}}$ = $\frac{2 \sqrt{7}}{7 \sqrt{7}} = \frac{2}{7}$ . Clearly, $\frac{2}{7}$ is a rational number.
Hence, $\frac{2 \sqrt{7}}{7 \sqrt{7}}$ is a rational number.

(iv) $\frac{1}{\sqrt{2}}$

We have
$\frac{1}{\sqrt{2}}$ = $\frac{1 \times \sqrt{2}}{\sqrt{2} \times \sqrt{2}}$ = $\frac{\sqrt{2}}{2}$ is an irrational number as the quotient obtained by dividing an irrational number by a rational number is an irrational number.

(v) $2 π$

$2 π$ is an irrational number. It is because $π$ is an irrational number.

(i) $(3 + \sqrt{3}) (2 + \sqrt{2})$

We have
$(3 + \sqrt{3}) (2 + \sqrt{2})$
= $3 (2 + \sqrt{2}) + \sqrt{3} (2 + \sqrt{2})$
= $6 + 3 \sqrt{2} + 2 \sqrt{3} + \sqrt{3 \times 2}$
= $6 + 3 \sqrt{2} + 2 \sqrt{3} + \sqrt{6}$

(ii) $(3 + \sqrt{3}) (3 - \sqrt{3})$

We have
$(3 + \sqrt{3}) (3 - \sqrt{3})$
= $3^{2} - {(\sqrt{3})}^{2}$ ... $[∵ (a + b) (a - b) = a^{2} - b^{2}]$
= $9 - 3$
= $6$

(iii) ${(\sqrt{5} + \sqrt{2})}^{2}$

We have
${(\sqrt{5} + \sqrt{2})}^{2}$
= ${(\sqrt{5})}^{2} + 2 \times \sqrt{5} \times \sqrt{2} + {(\sqrt{2})}^{2}$ ... $[∵ {(a + b)}^{2} = a^{2} + 2 a b + b^{2}]$
= $5 + 2 \sqrt{5 \times 2} + 2$
= $7 + 2 \sqrt{10}$

(iv) $(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2})$

We have
$(\sqrt{5} + \sqrt{2}) (\sqrt{5} - \sqrt{2})$
= ${(\sqrt{5})}^{2} - {(\sqrt{2})}^{2}$ ... $[∵ (a + b) (a - b) = a^{2} - b^{2}]$
= $5 - 2$
= $3$

3. Recall, $π$ is defined as the ratio of the circumference (say c) to its diameter (say d). That is, $π = \frac{c}{d}$ . This seems to contradict the fact that $π$ is irrational. How will you resolve this contradiction?

4. Represent $\sqrt{9.3}$ on the number line.

(i) $\frac{1}{\sqrt{7}}$

(ii) $\frac{1}{\sqrt{7} - \sqrt{6}}$

(iii) $\frac{1}{\sqrt{5} + \sqrt{2}}$

(iv) $\frac{1}{\sqrt{7} - 2}$