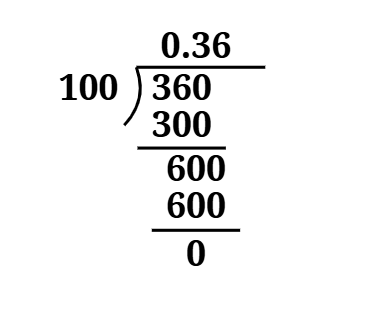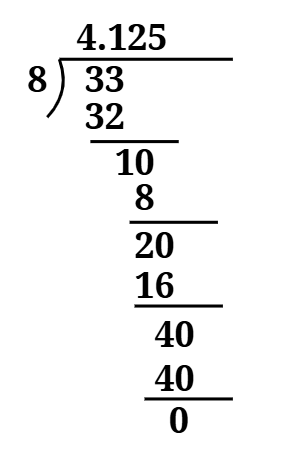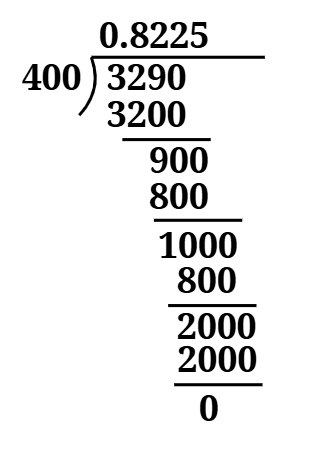Exercise 1.3 NCERT Class 9 Best Solutions

Exercise 1.1 Exercise 1.2 Exercise 1.3 Exercise 1.4 Exercise 1.5 Exercise 2.1 Exercise 2.2 Exercise 2.3 Exercise 2.4

Exercise 1.3 NCERT Class 9 contains a total of nine questions. All questions are based on the topic of real numbers and their decimal expansions.

Download NCERT Class 9 Book

Exercise 1.3 NCERT Class 9 Mathematics Solutions

Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9

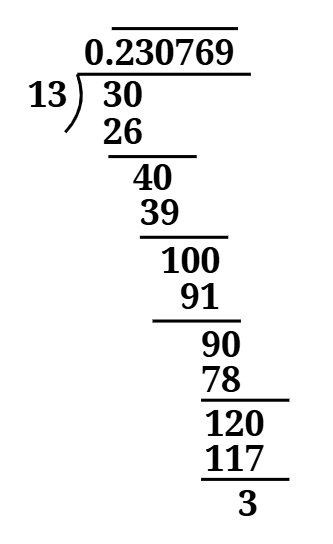
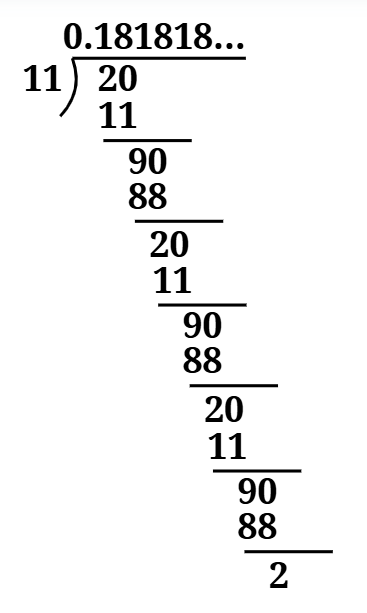
The first question of Exercise 1.3 NCERT Class 9 is about decimal form and their kind of decimal expansion.

1. Write the following in decimal form and say what kind of decimal expansion each has:

(i) $\frac{36}{100}$

Answer

The decimal expansion of $\frac{36}{100}$ is 0.36.
Since the remainder is zero, it is a terminating decimal expansion.

(ii) $\frac{1}{11}$

Answer

The decimal expansion of $\frac{1}{11}$ is 0.090909... = 0.09.
Since the remainder is not zero, it is a non-terminating and recurring decimal expansion.

(iii) $4 \frac{1}{8}$

Answer

∵ $4 \frac{1}{8} = \frac{33}{8}$
The decimal expansion of $\frac{33}{8}$ is 4.125.
Since the remainder is not zero, it is a terminating decimal expansion.

(iv) $\frac{3}{13}$

Answer

The decimal expansion of $\frac{3}{13}$ is 0.230769.
Since the remainder is not zero, it is a non-terminating and recurring decimal expansion.

(v) $\frac{2}{11}$

Answer

The decimal expansion of $\frac{2}{11}$ is 0.181818... = 0.18.
Since the remainder is not zero, it is a non-terminating and recurring decimal expansion.

(vi) $\frac{329}{400}$

Answer

The decimal expansion of $\frac{329}{400}$ is 0.8225.
Since the remainder is zero, it is a terminating decimal expansion.

The second question of Exercise 1.3 NCERT Class 9 is wholly about the decimal expansion of $\frac{1}{7}$ .

2. You know that $\frac{1}{7}$ = 0.142857. Can you predict what the decimal expansions of $\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$ are, without actually doing the long division? If so, how?

Answer

Yes, we can predict the decimal expansion of $\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$ by just using the decimal expansion of $\frac{1}{7}$ .

We have $\frac{1}{7}$ = 0.142857. Here, we can see that (142857) is the repeating block of digits. We can imagine this as given in the image below.

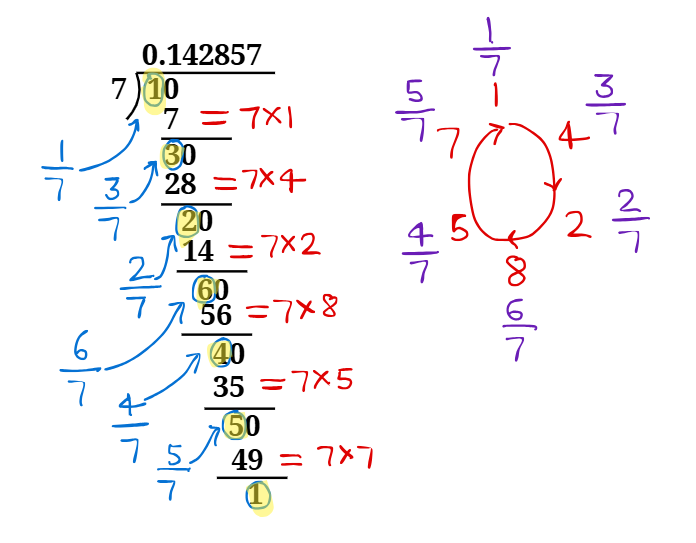
We can write:
$\frac{2}{7} = 2 \times \frac{1}{7}$ = 0.285714
Here, you only need to find first decimal 2 and other decimals can be written in cyclic order from the decimal expansion of $\frac{1}{7}$ = 0.142857.

Similarly,
$\frac{3}{7} = 3 \times \frac{1}{7}$ = 0.428571.
$\frac{4}{7} = 4 \times \frac{1}{7}$ = 0.571428.
$\frac{5}{7} = 5 \times \frac{1}{7}$ = 0.714285.
$\frac{6}{7} = 6 \times \frac{1}{7}$ = 0.857142.

The third question of Exercise 1.3 NCERT Class 9 is about the conversion of decimal form of a number to a $\frac{p}{q}$ form.

3. Express the following in the form $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \neq 0$ .

(i) 0.6

Answer

Let $x$ = 0.6
$\Rightarrow x = 0.666 . . .$ ----->(1)
$\Rightarrow 10 x = 6.666 . . .$ ----->(2)
Why? How?Multiplying by 10 on both sides

Subtracting equation (1) from equation (2), we get
$10 x = 6.666 . . .$
$x = 0.666 . . .$

$9 x = 6.000 . . .$
$\Rightarrow 9 x = 6$ .
$\Rightarrow x = \frac{6}{9}$ .
$\Rightarrow x = \frac{2}{3}$ .

Hence, 0.6 = $\frac{2}{3}$

(ii) 0.47

Answer

Let $x$ = 0.47
$\Rightarrow x = 0.4777 . . .$ ----->(1)
$\Rightarrow 10 x = 4.7777 . . .$ ----->(2)
Why? How?Multiplying by 10 on both sides; We can put 7 any number of times.

Subtracting equation (1) from equation (2)
$10 x = 4.7777 . . .$
$x = 0.4777 . . .$

$9 x = 4.3000 . . .$
$\Rightarrow 9 x = 4.3$ .
$\Rightarrow x = \frac{4.3}{9}$ .
$\Rightarrow x = \frac{4.3 \times 10}{9 \times 10} = \frac{43}{90}$ .

Hence, 0.47 = $\frac{43}{90}$ .

(iii) 0.001

Answer

Let $x$ = 0.001
$\Rightarrow x = 0.001001001 . . .$ ----->(1)
$\Rightarrow 1000 x = 1.001001001 . . .$ ----->(2)
Why? How?We multiply by 1000 on both sides because number of digits having bar is 3.

Subtracting equation (1) from equation (2), we get
$1000 x = 1.001001001 . . .$
$x = 0.001001001 . . .$

$999 x = 1.000000000 . . .$
$\Rightarrow 999 x = 1$ .
$\Rightarrow x = \frac{1}{999}$ .

Hence, 0.001 = $\frac{1}{999}$

The fourth question of Exercise 1.3 NCERT Class 9 is about the conversion of decimal form of a number to a $\frac{p}{q}$ form.

4. Express 0.99999... in the form $\frac{p}{q}$ . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Answer

Let $x$ = 0.99999 . .
$\Rightarrow x = 0.999 . . .$ ----->(1)
$\Rightarrow 10 x = 9.999 . . .$ ----->(2)
Why? How?We multiply by 10 as only one digit is repeated in the decimal expansion.

Subtracting equation (1) from equation (2), we get
$10 x = 9.999 . . .$
$x = 0.999 . . .$

$9 x = 9.000 . . .$
$\Rightarrow 9 x = 9$ .
$\Rightarrow x = \frac{9}{9}$ .
$\Rightarrow x = 1$ .

Hence, 0.9 = $1$ .
Here , 0.99999 . . . = 1, as we have number of 9's infinite and it resembles equal to 1 as we round-off.

The fifth question of Exercise 1.3 NCERT Class 9 is about the conversion of decimal form of a number to a $\frac{p}{q}$ form.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.

Answer

$∵ \frac{1}{17}$ = 0.0588235294117647.
There is a block of 16 digits [0588235294117647] that are repeating in the decimal expansion of $\frac{1}{17}$ .
Clearly, the maximum number of digits that repeat in the decimal expansion of a fraction is always less than its denominator.

The sixth question of Exercise 1.3 NCERT Class 9 is about finding the property of the denominators of rational numbers.

6. Look at several examples of rational numbers in the form $\frac{p}{q} (q \neq 0)$ , where $p$ and $q$ are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property $q$ must satisfy?

Answer

Below are given the several examples of rational numbers in the form $\frac{p}{q}$ , $q \neq 0$ , where $p$ and $q$ are integers with common factors other than 1 and having terminating decimal expansions.

$\frac{1}{2} = 0.5$ , here the factorization of the denominator 2 = 2×1 = $2^{1}$ .

$\frac{3}{4} = 0.75$ , here the factorization of the denominator 4 = 2×2×1 = $2^{2}$ .

$\frac{3}{10} = 0.3$ , here the factorization of the denominator 10 = 2×5×1 = $2^{1} \times 5^{1}$ .

$\frac{7}{25} = 0.28$ , here the factorization of the denominator 25 = 5×5×1 = $5^{2}$ .

$\frac{7}{40} = 0.175$ , here the factorization of the denominator 40 = 2×2×2×5×1 = $2^{3} \times 5^{1}$ .

$\frac{13}{100} = 0.13$ , here the factorization of the denominator 100 = 2×2×5×5×1 = $2^{2} \times 5^{2}$ .

$\frac{17}{1250} = 0.0136$ , here the factorization of the denominator 1250 = 2×5×5×5×5×1 = $2^{1} \times 5^{4}$ .

$\frac{83}{1000} = 0.083$ , here the factorization of the denominator 1000 = 2×2×2×5×5×5×1 = $2^{3} \times 5^{3}$ .

$\frac{79}{5000} = 0.0158$ , here the factorization of the denominator 5000 = 2×2×2×5×5×5×5×1 = $2^{3} \times 5^{4}$ .

$\frac{23}{625} = 0.0368$ , here the factorization of the denominator 625 = 5×5×5×5×1 = $5^{4}$ .

Conclusion: Property of q
From the examples given above, we can conclude that the denominator $q$ of a rational number $\frac{p}{q}$ having terminating decimal expansion must possess 2 or 5 as its only factors. In other words, $q = 2^{m} \times 5^{n}$ .

The seventh question of Exercise 1.3 NCERT Class 9 is about numbers whose decimal expansions are non-terminating non-recurring.

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Answer

Three numbers whose decimal expansions are non-terminating non-recurring can be any three of the following.

$\sqrt{2}, \sqrt{3}, \sqrt{5}, π, \sqrt[3]{3}, \sqrt[3]{2}, \sqrt[3]{7}, 2 \sqrt{2}, 5 \sqrt{3}, 7 \sqrt[3]{4}, . . . etc$ .

0.101001000100001..., 2.202002000200002..., 0.03003000300003..., 4.1311311131111...etc.

You can take any of the following group of numbers as these are all irrational numbers:

Square roots of prime numbers
$\sqrt{2}, \sqrt{3}, \sqrt{5}, \sqrt{7}, \sqrt{11}, \sqrt{13}, \sqrt{17}, . . . etc$ .

Square roots of composite numbers that are not perfect squares
$\sqrt{6}, \sqrt{8}, \sqrt{10}, \sqrt{12}, \sqrt{14}, \sqrt{15}, \sqrt{18}, . . . etc$ .

Cube roots of prime numbers
$\sqrt[3]{2}, \sqrt[3]{3}, \sqrt[3]{5}, \sqrt[3]{7}, \sqrt[3]{11}, \sqrt[3]{13}, \sqrt[3]{17}, . . . etc$ .

Cube roots of composite numbers that are not perfect cubes
$\sqrt[3]{4}, \sqrt[3]{6}, \sqrt[3]{9}, \sqrt[3]{10}, \sqrt[3]{12}, \sqrt[3]{14}, \sqrt[3]{15}, . . . etc$ .

Fourth roots of prime numbers
$\sqrt[4]{2}, \sqrt[4]{3}, \sqrt[4]{5}, \sqrt[4]{7}, \sqrt[4]{11}, \sqrt[4]{13}, \sqrt[4]{17}, . . . etc$ .

Similarly, you can find infinitely many irrational numbers whose decimal expansion is non-terminating and non-recurring. You must also know that the numbers of the following form are also irrational numbers.

$2^{\frac{2}{3}}, 2^{\frac{4}{3}}, 2^{\frac{5}{3}}, 3^{\frac{2}{3}}, 7^{\frac{2}{3}}, 15^{\frac{5}{6}}, . . . etc$ .

The eighth question of Exercise 1.3 NCERT Class 9 is about irrational numbers lying between two rational numbers.

8. Find three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$ .

Answer

Decimal expansion of $\frac{5}{7}$ and $\frac{9}{11}$ are
$\frac{5}{7}$ = 0.714285 = 0.714285714285...
$\frac{9}{11}$ = 0.81 = 0.81818181...

Here, 0.71 < 0.72 < 0.73 < 0.74 < 0.75 < 0.76 < 0.77 < 0.78 < 0.79 < 0.80 < 0.81

Clearly, three irrational numbers between 0.7142857142857... and 0.81818181... are
(i) 0.75075007500075000075...
(ii) 0.7670767007670007670000767...
(iii) 0.808008000800008000008...

Similarly, you can find infinitely many irrational numbers. Other irrational numbers between $\frac{5}{7}$ and $\frac{9}{11}$ are :

0.72072007200072000072...
0.7303003000300003000003...
0.741741174111741111...
0.7434743434743434743434...
0.74074007400074000074...

The ninth question of Exercise 1.3 NCERT Class 9 is about classifying whether a number is rational or irrational.

9. Classify the following numbers as rational or irrational:

(i) $\sqrt{23}$

Answer

Irrational, as 23 is not a perfect square and it is also a prime number.

(ii) $\sqrt{225}$

Answer

$∵ \sqrt{225} = \sqrt{3×3×5×5} = 15$ .
Rational.

(iii) 0.3796

Answer

Rational as 0.3796 is a terminating decimal expansion.

(iv) 7.478478...

Answer

Since 7.478478... = 7.478. The block of digits '4', '7', '8' repeats in the number. So, it is a non-terminating and recurring decimal expansion.
Hence, 7.478478... is a Rational Number.

(v) 1.101001000100001...

Answer

Irrational , as it is a non-terminating and non-recurring decimal expansion.

Chapter Test ML Aggarwal Class 9 Rational and Irrational Numbers Full Solutions

07/07/2025 No Comments

Exercise 1.5 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

04/07/2025 No Comments

Exercise 1.4 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

01/07/2025 No Comments

Polynomial Worksheets Class 9 Mathematics Best for Practice

30/06/2025 No Comments

Exercise 1.3 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

25/06/2025 No Comments

Motion NCERT Class 9 Concise Notes and Best Question Answers

16/06/2025 No Comments

Download NCERT Class 9 Book

Exercise 1.3 NCERT Class 9 Mathematics Solutions

1. Write the following in decimal form and say what kind of decimal expansion each has:

(i) 36100

Answer

(ii) 111

Answer

(iii) 418

Answer

(iv) 313

Answer

(v) 211

Answer

(vi) 329400

Answer

2. You know that 17 = 0.142857. Can you predict what the decimal expansions of 27,37,47,57,67 are, without actually doing the long division? If so, how?

Answer

3. Express the following in the form pq, where p and q are integers and q≠0.

(i) 0.6

Answer

(ii) 0.47

Answer

(iii) 0.001

Answer

4. Express 0.99999... in the form pq. Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Answer

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 117? Perform the division to check your answer.

Answer

6. Look at several examples of rational numbers in the form pq(q≠0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Answer

7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Answer

8. Find three different irrational numbers between the rational numbers 57 and 911.

Answer

9. Classify the following numbers as rational or irrational:

(i) 23

Answer

(ii) 225

Answer

(iii) 0.3796

Answer

(iv) 7.478478...

Answer

(v) 1.101001000100001...

Answer

Chapter Test ML Aggarwal Class 9 Rational and Irrational Numbers Full Solutions

Exercise 1.5 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Exercise 1.4 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Polynomial Worksheets Class 9 Mathematics Best for Practice

Exercise 1.3 ML Aggarwal Class 9 ICSE Mathematics Chapter 1 Rational and Irrational Numbers Best Solutions

Motion NCERT Class 9 Concise Notes and Best Question Answers

(i) $\frac{36}{100}$

(ii) $\frac{1}{11}$

(iii) $4 \frac{1}{8}$

(iv) $\frac{3}{13}$

(v) $\frac{2}{11}$

(vi) $\frac{329}{400}$

2. You know that $\frac{1}{7}$ = 0.142857. Can you predict what the decimal expansions of $\frac{2}{7}, \frac{3}{7}, \frac{4}{7}, \frac{5}{7}, \frac{6}{7}$ are, without actually doing the long division? If so, how?

3. Express the following in the form $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \neq 0$ .

4. Express 0.99999... in the form $\frac{p}{q}$ . Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of $\frac{1}{17}$ ? Perform the division to check your answer.

6. Look at several examples of rational numbers in the form $\frac{p}{q} (q \neq 0)$ , where $p$ and $q$ are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property $q$ must satisfy?

8. Find three different irrational numbers between the rational numbers $\frac{5}{7}$ and $\frac{9}{11}$ .

(i) $\sqrt{23}$

(ii) $\sqrt{225}$