Exercise 1.1 NCERT Class 9 Solutions

Exercise 1.1 NCERT Class 9 Mathematics Solutions

Exercise 1.1 NCERT Class 9 from the chapter Number Systems contains 4 questions.
In this exercise, the questions are based on topics such as natural numbers, whole numbers, integers, rational numbers and irrational numbers.

Download NCERT Class 9 Book

The first question of Exercise 1.1 NCERT Class 9 is about rational numbers.

1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \neq 0$ ?

Answer

Yes, zero is a rational number.
Yes, we can write 0 in the form $\frac{p}{q}$ as follows:
$0 = < \frac{0}{1}$ , where $p = 0$ and $q = 1$ , which is not equal to zero.

The second question of Exercise 1.1 NCERT Class 9 is about finding rational numbers between two natural numbers.

2. Find six rational numbers between 3 and 4.

Answer

Method 1: By finding the middle numbers
In this method, a rational number can be easily obtained between two rational numbers by adding the two rational numbers and dividing by 2 subsequently. The rational number obtained by this method lies in the middle of the two given rational numbers.
1st rational number between 3 and 4 = $\frac{3 + 4}{2} = \frac{7}{2}$ .

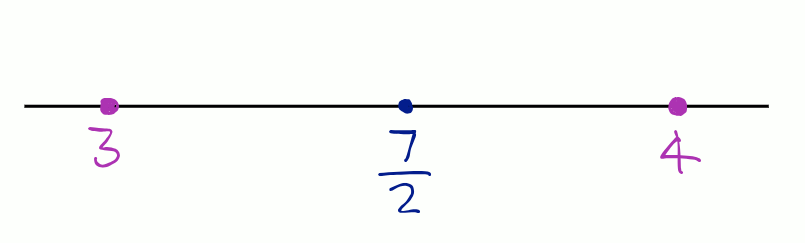
2nd rational number between 3 and 4 = $\frac{3 + \frac{7}{2}}{2} =$ $\frac{\frac{6 + 7}{2}}{2} = \frac{13}{4}$ .

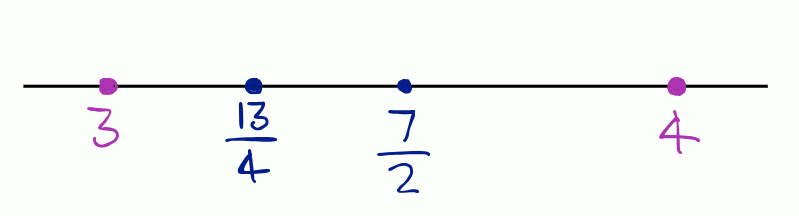
3rd rational number between 3 and 4 = $\frac{\frac{7}{2} + 4}{2} = \frac{\frac{7 + 8}{2}}{2} = \frac{15}{4}$ .

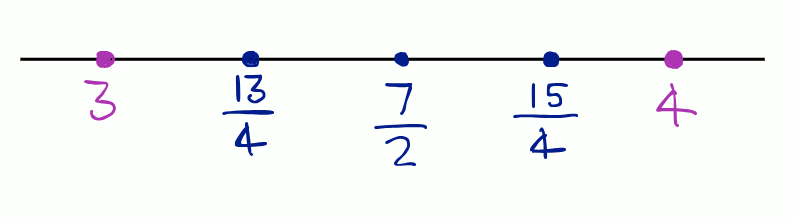
4th rational number between 3 and 4 = $\frac{3 + \frac{13}{4}}{2} = \frac{\frac{25}{4}}{2} = \frac{25}{8}$ .

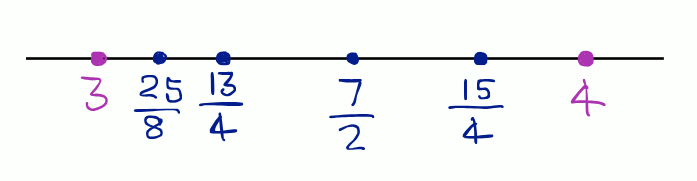
5th rational number between 3 and 4 = $\frac{\frac{13}{4} + \frac{7}{2}}{2} = \frac{\frac{13 + 14}{4}}{2} = \frac{27}{8}$ .

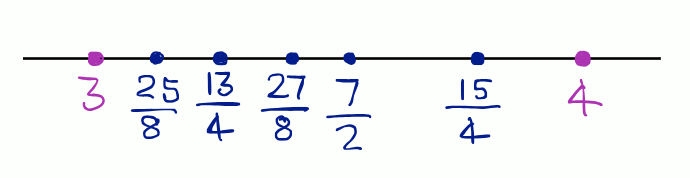
6th rational number between 3 and 4 = $\frac{\frac{7}{2} + \frac{15}{4}}{2} = \frac{\frac{14 + 15}{4}}{2} = \frac{29}{8}$

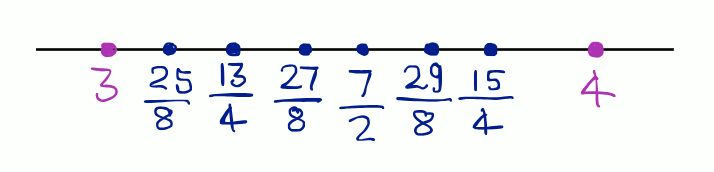
Method 2: Numerator Gap Method
In this method, we choose an appropriate number and multiply the numerator and denominator of both the numbers to increase the gap between the numerators. We usually choose that appropriate number to be one more than the number of rational numbers to be found.
Since we have to find 6 rational numbers between 3 and 4.
We can write,
3 = $\frac{3 \times (6 + 1)}{(6 + 1)} = \frac{3 \times 7}{7} = \frac{21}{7}$ ,
4 = $\frac{4 \times (6 + 1)}{(6 + 1)} = \frac{4 \times 7}{7} = \frac{28}{7}$ .
∵ The six rational numbers between 3 and 4 is equivalent to the six rational numbers between $\frac{21}{7}$ and $\frac{28}{7}$ .
So, we can write,
$\frac{21}{7} < \frac{22}{7} < \frac{23}{7} < \frac{24}{7} < \frac{25}{7} < \frac{26}{7} < \frac{27}{7} < \frac{28}{7}$ .
Hence, Six rational numbers between 3 and 4 are $\frac{22}{7}, \frac{23}{7}, \frac{24}{7}, \frac{25}{7}, \frac{26}{7}, \frac{27}{7}$ .

The third question of Exercise 1.1 NCERT Class 9 is about finding rational numbers between two rational numbers.

3. Find five rational numbers between $\frac{3}{5}$ and $< \frac{4}{5}$ .

Answer

Method 1: By finding the middle numbers
In this method, a rational number can be easily obtained between two rational numbers by adding the two rational numbers and dividing by 2 subsequently. The rational number obtained by this method lies in the middle of the two given rational numbers.
1st rational number between $\frac{3}{5}$ and $\frac{4}{5}$ = $\frac{\frac{3}{5} + \frac{4}{5}}{2} = \frac{\frac{7}{5}}{2} = \frac{7}{10}$

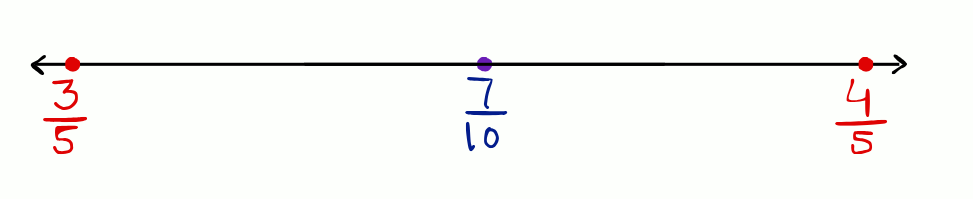
2nd rational number between $\frac{3}{5}$ and $\frac{4}{5}$ = $\frac{\frac{3}{5} + \frac{7}{10}}{2} = \frac{\frac{13}{10}}{2} = \frac{13}{20}$

3rd rational number between $\frac{3}{5}$ and $\frac{4}{5}$ = $\frac{\frac{7}{10} + \frac{4}{5}}{2} = \frac{\frac{15}{10}}{2} = \frac{15}{20}$

4th rational number between $\frac{3}{5}$ and $\frac{4}{5}$ = $\frac{\frac{3}{5} + \frac{13}{20}}{2} = \frac{\frac{25}{20}}{2} = \frac{25}{40} = \frac{5}{8}$

5th rational number between $\frac{3}{5}$ and $\frac{4}{5}$ = $\frac{\frac{13}{20} + \frac{7}{10}}{2} = \frac{\frac{27}{20}}{2} = \frac{27}{40}$

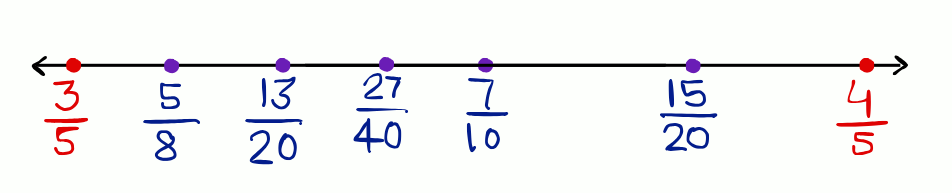
6th rational number between $\frac{3}{5}$ and $\frac{4}{5}$ = $\frac{\frac{7}{10} + \frac{15}{20}}{2} = \frac{\frac{29}{20}}{2} = \frac{29}{40}$

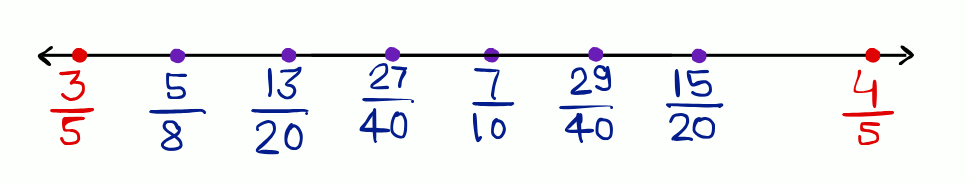
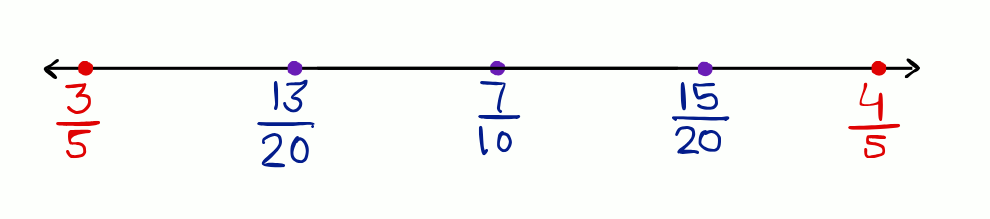
Method 2: Numerator Gap Method
In this method, we choose an appropriate number and multiply the numerator and denominator of both the numbers to increase the gap between the numerators. We usually choose that appropriate number to be one more than the number of rational numbers to be found.
Since we have to find 6 rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ .
We can write,
$\frac{3}{5}$ = $\frac{3 \times (6 + 1)}{5 \times (6 + 1)} = \frac{3 \times 7}{5 \times 7} = \frac{21}{35}$ ,
$\frac{4}{5}$ = $\frac{4 \times (6 + 1)}{5 \times (6 + 1)} = \frac{4 \times 7}{5 \times 7} = \frac{28}{35}$ .
∵ The six rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ is equivalent to the six rational numbers between $\frac{21}{35}$ and $\frac{28}{35}$ .
So, we can write,
$\frac{21}{35} < \frac{22}{35} < \frac{23}{35} < \frac{24}{35} < \frac{25}{35} < \frac{26}{35} < \frac{27}{35} < \frac{28}{35}$ .
Hence, Six rational numbers between $\frac{3}{5}$ and $\frac{4}{5}$ are $\frac{22}{35}, \frac{23}{35}, \frac{24}{35}, \frac{25}{35}, \frac{26}{35}, \frac{27}{35}$ .
Don't be confused if different answers are obtained with different methods. It is because rational numbers are infinite between any two numbers. So, you can arrive to an infinite number of answers in these type of questions.

The fourth question of Exercise 1.1 NCERT Class 9 is true/false question on the number system.

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

Answer

True, as every natural number like 1, 2, 3, 4, 5, ... , etc. lies in the set of whole numbers {0, 1, 2, 3, 4, 5, ... }.

(ii) Every integer is a whole number.

Answer

False, as the negative numbers such as −1, −2, −3, ..., etc. does not belong to the set of whole numbers {0, 1, 2, 3, 4, 5, ... }

(iii) Every rational number is a whole number.

Answer

False, as fractions such as $\frac{1}{2}, \frac{2}{5}, \frac{7}{9}, \frac{−8}{3}, ...$ etc. are not whole numbers.

Exercise 1.1 NCERT Class 9 Mathematics Solutions

Download NCERT Class 9 Book

1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \neq 0$ ?

Answer

2. Find six rational numbers between 3 and 4.

Answer

3. Find five rational numbers between $\frac{3}{5}$ and $< \frac{4}{5}$ .

Answer

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

Answer

(ii) Every integer is a whole number.

Answer

(iii) Every rational number is a whole number.

Answer

Related Worksheets

Related Links 🔗

Exercise 1.1 NCERT Class 9 Mathematics Solutions

Download NCERT Class 9 Book

1. Is zero a rational number? Can you write it in the form pq , where p and q are integers and q≠0?

Answer

2. Find six rational numbers between 3 and 4.

Answer

3. Find five rational numbers between 35 and <45.

Answer

4. State whether the following statements are true or false. Give reasons for your answers.

(i) Every natural number is a whole number.

Answer

(ii) Every integer is a whole number.

Answer

(iii) Every rational number is a whole number.

Answer

Related Worksheets

Related Links 🔗

1. Is zero a rational number? Can you write it in the form $\frac{p}{q}$ , where $p$ and $q$ are integers and $q \neq 0$ ?

3. Find five rational numbers between $\frac{3}{5}$ and $< \frac{4}{5}$ .