Exercise 2.2 NCERT Class 11
Q.1 Q.2 Q.3 Q.4 Q.5 Q.6 Q.7 Q.8 Q.9

Exercise 2.2 NCERT Class 11 from chapter Relations and Functions contains 9 questions.
In this exercise, the questions are based on the topic "Relations and Functions".

Download NCERT Class 11 Book

Exercise 2.2 NCERT Class 11 Mathematics Solutions

The first question of Exercise 2.2 NCERT Class 11 is related to relations, domain, codomain and range.

1. Let A = {1, 2, 3, . . ., 14}. Define a relation R from A to A by R={(x,y):3x−y=0,wherex,y∈A}. Write down its domain, codomain and range.

It is given that
A = {1, 2, 3, . . ., 14} and
R = {(x,y):3x−y=0,wherex,y∈A}
From the given definition of R, we can deduce that R contains all those ordered pairs of A×A in which three times the first element equals the second element.
∵3x−y=0
⇒3x=y
i.e. 3 times the first element equals the second element.
∴ R can be written in roster form as
R = {(1, 3), (2, 6), (3, 9), (4, 12)}
∵ Domain is the set of all the first elements of the ordered pairs in R.
∴ Domain of R = {1, 2, 3, 4}
∵ Range is the set of all the second elements of the ordered pairs in R.
∴ Range of R = {3, 6, 9, 12}
∵ Codomain is the set A itself.
∴ Codomain of R = {1, 2, 3, 4, . . . , 14}

The second question of Exercise 2.2 NCERT Class 11 is related to relation and roster form of sets.

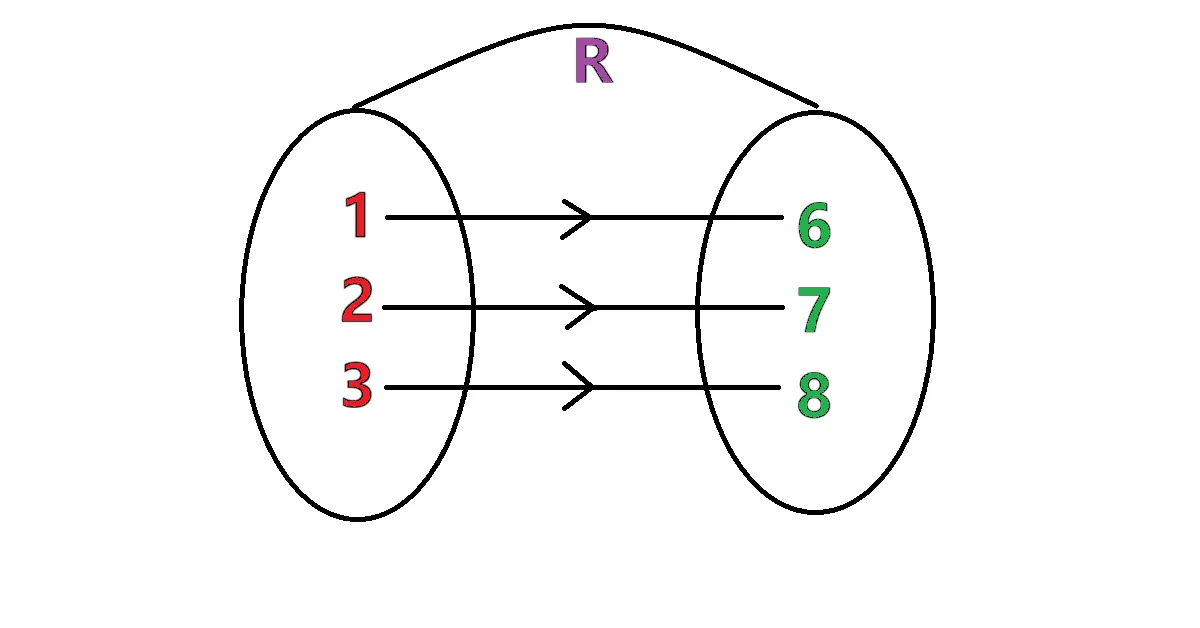
2. Define a relation R on the set N of natural numbers by R={(x,y):y=x+5,x is a natural number less than 4; x,y∈N}. Depict this relationship using roster form. Write down the domain and the range.

∵ R = {(x,y):y=x+5,x is a natural number less than 4;x,y∈N
Here, we can take x=1,2,3. It is because x is a natural number less than 4.
Corresponding values of y = 6,7,8 respectively.
∴ R = {(1, 6), (2, 7), (3, 8)}
We know that domain is the set of the first elements of the ordered pairs and range is the set of the second elements of the ordered pair.
∴ Domain of R = {1, 2, 3}
& Range of R = {6, 7, 8}

Exercise 2.2 NCERT Class 11 Q.2
Depiction of R

The third question of Exercise 2.2 NCERT Class 11 is also related to relation and roster form of sets.

3. A = {1, 2, 3, 5} and B = {4, 6, 9}. Define a relation R from A to B by R={(x,y): the difference between x and y is odd; x∈A,y∈B}.Write R in roster form.

We have
A = {1, 2, 3, 5},
B = {4, 6, 9},
R = {(x,y):the difference betweenxandyis odd;x∈A,y∈A}
The ordered pairs of R can be obtained by taking an odd number from the set A and an even number from the set B or vice-versa.
The difference between x and y will automatically becomes odd.
Therefore, R in roster form can be written as:
R = {(1, 4), (1, 6), (2, 9), (3, 4), (3,6), (5, 4), (5, 6)}

The fourth question of Exercise 2.2 NCERT Class 11 is related to relation, roster and se-builder form of sets, domain and range.

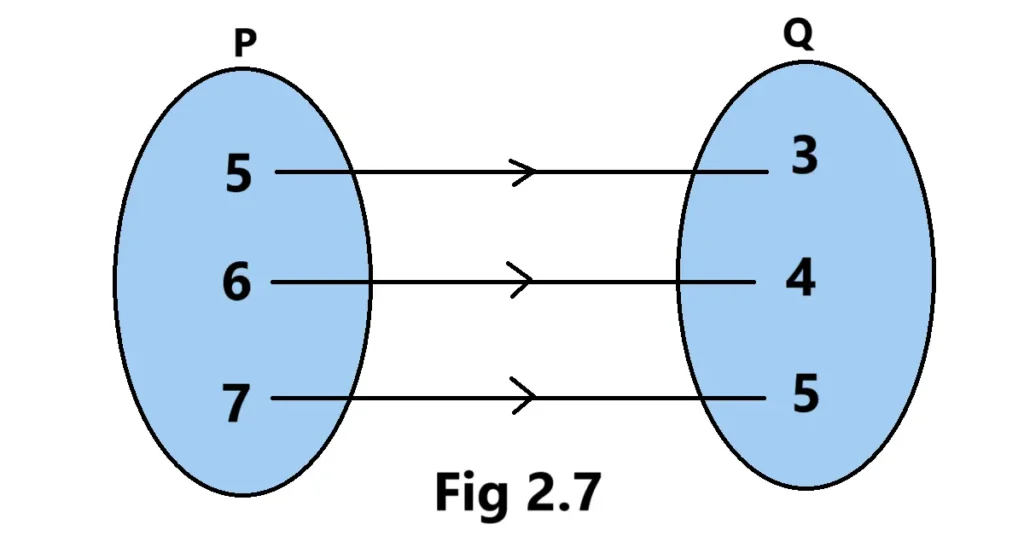
4. The Fig 2.7 shows a relationship between the sets P and Q. Write this relation
(i) in set-builder form (ii) roster form.
What is its domain and range?

Fig 2.7 Exercise 2.2 NCERT Class 11

(i) From the Fig 2.7, we can deduce that each element of Q can be obtained by subtracting 2 from the corresponding element of P.
So, if x is an element of P, then y=x−2 is an element of Q.
Thus, the relation R in set-builder form is given by
R = {(x,y):y=x−2;4<x<8;x∈N}

(ii) The relation R in roster form is as follows:
R = {(5, 3), (6, 4), (7, 5)}
Domain of R = {5, 6, 7}
Range of R = {3, 4, 5}

The fifth question of Exercise 2.2 NCERT Class 11 is related to relation, roster and se-builder form of sets, domain and range.

5. Let A = {1, 2, 3, 4, 6}. Let R be the relation on A defined by
{(a,b):a,b∈A,b is exactly divisible by a}.
(i) Write R in roster form
(ii) Find the domain of R
(iii) Find the range of R.

We have,
A = {1, 2, 3, 4, 6}
R = {(a,b):a,b∈A,b is exactly divisible bya}
Here, R is a subset of A×A, the second element of each ordered pair in R is exactly divisible by the first element.

(i) R in roster form is as follows:
R = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 6), (2, 2), (2, 4), (2, 6), (3, 3), (3, 6), (4, 4), (6, 6)}

(ii) Domain of R = {1, 2, 3, 4, 6}

(iii) Range of R = {1, 2, 3, 4, 6}

The sixth question of Exercise 2.2 NCERT Class 11 is related to domain and range.

6. Determine the domain and range of the relation R defined by
R = {(x,x+5):x∈ {0,1,2,3,4,5}}.

The given relation is
R = {(x,x+5):x∈ {0,1,2,3,4,5}}.
We can write R in roster form as follows:
R = {(0, 0+5), (1, 1+5), (2, 2+5), (3, 3+5), (4, 4+5), (5, 5+5)}.
={(0, 5), (1, 6), (2, 7), (3, 8), (4, 9), (5, 10)}.
Clearly,
Domain of R = {0, 1, 2, 3, 4, 5}.
Range of R = {5, 6, 7, 8, 9, 10}.

The seventh question of Exercise 2.2 NCERT Class 11 is related to relations and roster form.

7. Write the relation
R = {(x,x3):x is a prime number less than 10} in roster form.

The given relation is
R = {(x,x3):x is a prime number less than 10}
R in roster form is as follows:
R = {(2, 23), (3, 33), (5, 53), (7, 73)}
  = {(2, 8), (3, 27), (5, 125), (7, 343)}

The eighth question of Exercise 2.2 NCERT Class 11 is related to finding number of relations.

8. Let A = {x,y,z} and B = {1, 2}. Find the number of relations from A to B.

We have,
A = {x,y,z} and B = {1, 2}.
∵ n(A) = 3 & n(B) = 2.
∴ n(A×B) = n(A) × n(B) = 3 × 2 = 6.
Now, number of relations from A to B
    = number of subsets of A×B.
    = 2n(A×B)
    = 26
    = 2×2×2×2×2×2
    = 64.
Hence, the number of relations from set A to set B are 64.

The ninth question of Exercise 2.2 NCERT Class 11 is related to domain and range of relations.

9. Let R be the relation on Z defined by
R={(a,b):a,b∈Z,a−b is an integer}. Find the domain and range of R.

We have
R={(a,b):a,b∈Z,a−b is an integer}.
The set contains all ordered pairs in which the difference of the elements of the ordered pair is an integer. But, we know that the difference of two integers is always an integer.
So, a and b are integers.

The domain of R is the set of the first elements of the ordered pairs (a,b).
And the range of R is the set of the second elements of the ordered pairs.
Hence, the domain and range of R is the set of integers.